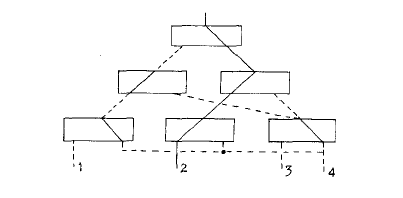
The change is a dramatic one, for the fact that the original problem was to identify the maximum value among four given values is no longer reflected in the "topology" of the rules of behaviour: in Fig.7 we only find the number "4" mentioned once. By introducing another variable, say n, and replacing the "4" in Fig.7 by n we have suddenly the rules of behaviour to identify the maximum occurring among the n elements a[1], a[2], .......,a[n] and this practically only for the price that before application, the variable n must be put to its proper value.
I called the change a dramatic one, for now we have not only given rules of behaviour which must be interpreted sequentially —this was already the case with Fig.6— but we have devised a single mechanism for identifying the maximum value among any number of given elements, whereas our original non-sequential machine could only be built for a previously well-defined number of elements. We have mapped our comparisons in time instead of in space, and if we wish to compare the two methods, it is as if the sequential machine "extends itself" in terms of Fig.3 as the need arises. It is our last transition which displays the sequential processes in their full glory.
The technical term for what we have called "rules of behaviour" is an algorithm or a program. (It is not customary to call it "a sequential program" although this name would be fully correct.) Equipment able to follow such rules, "to execute such a program" is called "a general purpose sequential computer" or "computer" for short; what happens during such a program execution is called "a sequential process".
There is a commonly accepted technique of writing algorithms without the need of such pictures as we have used, viz. ALGOL 60 ("ALGOL" being short for Algorithmic Language). For a detailed discussion of ALGOL 60 I must refer the reader to the existing literature. We shall use it in future, whenever convenient for our purposes.
For the sake of illustration we shall describe the algorithm of Fig.7 (but for n instead of "4") by a sequence of ALGOL statements:
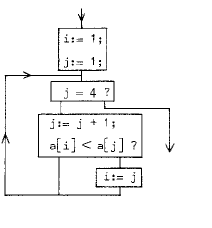
i:= 1; j:= 1;
back: if j ≠ n then
begin j:= j + 1;
if a[i] < a[j] then i:= j;
goto back
end .
The first two statements: "i:=l; j:= 1" are —I hope— self-explanatory. Then comes "back:", a so-called label, used to identify this place in the program. Then comes "if j ≠ n then", a so-called conditional clause. If the condition expressed by it is satisfied, the following statement will be performed, otherwise it will be skipped. (Another example of it can be found two lines lower.) When the extent of the program which may have to be skipped presents itself primarily as a sequence of more than one statement, then one puts the so-called statement brackets "begin" and "end" around this sequence, thereby making it into a single statement as far as its surroundings are concerned. (This is entirely analogous to the effect of parentheses in algebraic formulae, such as "a * (b + c)" where the parenthesis pair indicates that the whole expression contained within it is to be taken as factor.) The last statement "goto back" means that the process should be continued at the point thus labeled; it does exactly the same thing for us as the upward leading line of Fig.7.
2. Loosely Connected Processes.
The subject matter of this monograph is the cooperation between loosely connected sequential processes and this section will be devoted to a thorough discussion of a simple, but representative problem, in order to give the reader some feeling for the problems in this area.
In the previous section we have described the nature of a single sequential process, performing its sequence of actions autonomously, i.e. independent of its surroundings as soon as it has been started.
When two or more of such processes have to cooperate with each other, they must be connected, i.e. they must be able to communicate with each other in order to exchange information. As we shall see below, the properties of these means of intercommunication play a vital role.
Furthermore, we have stipulated that the processes should be connected loosely; by this we mean that apart from the (rare) moments of explicit intercommunication, the individual processes themselves are to be regarded as completely independent of each other. In particular we disallow any assumption about the relative speeds of the different processes. (Such an assumption —say"processes geared to the same clock"— could be regarded as implicit intercommunication.) This independence of speed ratios is in strict accordance with our appreciation of the single sequential process: its only essential feature is, that its elementary steps are performed in sequence. If we prefer to observe the performance with a chronometer in our hand, we may do so, but the process itself remains remarkably unaffected by this observation.
I warn the reader that my consistent refusal to make any assumptions about the speed ratios will at first sight appear as a mean trick to make things more difficult than they already are. I feel, however, fully justified in my refusal. Firstly, we may have to cope with situations in which, indeed, very little is known about the speeds. For instance, part of the system may be a manually operated input station, another part of the system might be such, that it can be stopped externally for any period of time, thus reducing its speed temporarily to zero. Secondly —and this is much more important— when we think that we can rely upon certain speed ratios, we shall discover that we have been "pound foolish and penny wise". True that certain mechanisms can be made simpler under the assumption of speed ratio restrictions. The verification, however, that such an assumption is always justified, is in general extremely tricky and the task to make, in a reliable manner, a well behaved structure out of many interlinked components is seriously aggravated when such "analogue interferences" have to be taken into account as well. (For one thing: it will make the proper working a rather unstable equilibrium, sensitive to any change in the different speeds, as may easily arise by replacement of a component by another —say, replacement of a line printer by a faster model— or reprogramming of a certain portion.)
2.1. A Simple Example.
After these introductory remarks I shall discuss the first problem.
We consider two sequential processes, "process 1" and "process 2", which for our purposes can be regarded as cyclic. In each cycle a so-called "critical section" occurs, critical in the sense that the processes have to be constructed in such a way, that at any moment at most one of the two is engaged in its critical section. In order to effectuate this mutual exclusion the two processes have access to a number of common variables. We postulate, that inspecting the present value of such a common variable and assigning a new value to such a common variable are to be regarded as indivisible, non-interfering actions. I.e. when the two processes assign a new value to the same common variable "simultaneously", then the assignments are to be regarded as done the one after the other, the final value of the variable will be one of the two values assigned, but never a "mixture" of the two. Similarly, when one process inspects the value of a common variable "simultaneously" with the assignment to it by the other one, then the first process will find either the old or the new value, but never a mixture.
For our purposes ALGOL 60 as it stands is not suited, as ALGOL 60 has been designed to describe one single sequential process. We therefore propose the following extension to enable us to describe parallellism of execution. When a sequence of statements —separated by semicolons as usual in ALGOL 60— is surrounded by the special statement bracket pair "parbegin" and "parend", this is to be interpreted as parallel execution of the constituent statements. The whole construction —let us call it "a parallel compound"— can be regarded as a statement. Initiation of a parallel compound implies simultaneous initiation of all its constituent statements, its execution is completed after the completion of the execution of all its constituent statements. E.g.:
begin S1; parbegin S2; S3; S4; parend; S5 end
(in which S1, S2, S3. S4 and S5 are used to indicate statements) means that after the completion of S1, the statements S2. S3 and S4 will be executed in parallel, and only when they are all finished, then the execution of statement 55 will be initiated.
With the above conventions we can describe our first solution:
begin integer turn; turn:= 1;
parbegin
process 1: begin Ll: if turn = 2 then goto Ll;
critical section 1;
turn:= 2;
remainder of cycle 1; goto L1
end;
process 2: begin L2: if turn = 1 then goto L2;
critical section 2;
turn:= 1;
remainder of cycle 2; goto L2
end
parend
end .
(Note for the inexperienced ALGOL 60 reader. After "begin" in the first line we find the so-called declaration "integer turn", thereby sticking to the rule of ALGOL 60 that program text is not allowed to refer to variables without having introduced them with the aid of a declaration. As this declaration occurs after the "begin" of the outermost statement bracket pair it means that for the whole duration of the program a variable has been introduced that will only take on integer values and to which the program text can refer by means of the name "turn".)
The two processes communicate with each other via the common integer "turn", the value of which indicates which of the two processes is the first to perform (or rather: to finish) its critical section. From the program it is clear that after the first assignment, the only possible values of the variable "turn" are 1 and 2. The condition for process 2 to enter its critical section is that it finds at some moment "turn ≠ 1", i.e. "turn = 2". But the only way in which the variable "turn" can get this value is by the assignment "turn:= 2" in process 1. As process 1 performs this assignment only at the completion of its critical section, process 2 can only initiate its critical section after the completion of critical section 1. And critical section 1 could indeed be initiated, because the initial condition "turn = 1" implied "turn ≠ 2", so that the potential wait cycle, labeled L1, was initially inactive. After the assignment "turn:= 2" the roles of the two processes are interchanged. (N.B. It is assumed that the only references to the variable "turn" are the ones explicitly shown in the program.)
Our solution, though correct, is, however, unnecessarily restrictive: after the completion of critical section 1, the value of the variable "turn" becomes "2", and it must be =1 again, before the next entrance into critical section 1. As a result the only admissible succession of critical sections is the strictly alternating one "1,2,1,2,1,2,1,.....", in other words, the two processes are synchronized. In order to stress explicitly that this is not the kind of solution we wanted, we impose the further condition "If one of the processes is stopped well outside its critical section, this is not allowed to lead to potential blocking of the other process.". This makes our previous solution unacceptable and we have to look for another.
Our second effort works with two integers "c1" and "c2", where c = 0 / 1 respectively will indicate that the corresponding process in inside / outside its critical section respectively. We may try the following construction:
begin integer c1, c2;
c1:= 1; c2:= 1;
parbegin
process1: begin L1: if c2 = 0 then goto L1;
c1: = 0;
critical section 1;
c1:= 1;
remainder of cycle 1; goto L1
end;
process2: begin L2: if c1 = 0 then goto L2;
c2: = 0;
critical section 2;
c2:= 1;
remainder of cycle 2; goto L2
end
parend
end .
The first assignments set both c's = 1, in accordance with the fact that the processes are started outside their critical sections. During the entire execution of critical section 1 the relation "c1 = 0" holds and the first line of process 2 is effectively a wait "Wait as long as process 1 is in its critical section.". The trial solution gives indeed some protection against simultaneity of critical section execution, but is, alas, too simple, because it is wrong. Let first process 1 find that c2 = 1; let process 2 inspect c1 immediately afterwards, then it will (still) find c1 = 1. Both processes, having found that the other is not in its critical section, will conclude that they can enter their own section safely!
We have been too optimistic, we must play a safer game. Let us invert, at the beginning of the parallel processes, the inspection of the "c" of the other and the setting of the own "c". We then get the construction:
begin integer c1, c2;
c1:= 1; c2:= 1;
parbegin
process 1: begin A1: c1:= 0;
L1: if c2 = 0 then goto Ll;
critical section 1;
c1:= 1;
remainder of cycle 1; goto A1
end;
process 2: begin A2: c2:= 0;
L2: if c1 = 0 then goto L2;
critical section 2;
c2:= 1;
remainder of cycle 2; goto A2
end
parend
end .
It is worth while to verify that this solution is at least completely safe. Let us focus our attention on the moment that process 1 finds c2 = 1 and therefore decides to enter its critical section. At this moment we can conclude
1) that the relation "c1 = 0" already holds and will continue to hold until process 1 has completed the execution of its critical section,
2) that, as "c2 = 1" holds, process 2 is well outside its critical section, which it cannot enter as long as "c1 = 0" holds, i.e. as long as process 1 is still engaged in its critical section.
Thus the mutual exclusion is indeed guaranteed.
But this solution, alas, must also be rejected: in its safety measures it has been too drastic, for it contains the danger of definite mutual blocking. When after the assignment "c1:= 0" but yet before the inspection of c2 (both by process 1) process 2 performs the assignment "c2:= 0" then both processes have arrived at label L1 or L2 respectively and both relations "c1 = 0" and "c2 = 0" hold, with the result that both processes will wait upon each other until eternity. Therefore also this solution must be rejected.
It was OK to set one's own "c" before inspecting the "c" of the other, but it was wrong to stick to one's own c-setting and just to wait. This is (somewhat) remedied in the following construction:
begin integer c1, c2;
c1:= 1; c2:= 1;
parbegin
process 1: begin L1: c1:= 0;
if c2 = 0 then
begin c1:= 1; goto L1 end;
critical section 1;
c1:= 1;
remainder of cycle 1; goto L1
end;
process 2: begin L2: c2:= 0;
if c1 = 0 then
begin c2:= 1; goto L2 end;
critical section 2;
c2:= 1;
remainder of cycle 2; goto L2
end
parend
end .
This construction is as safe as the previous one and, when the assignments "c1:= 0" and "c2:= 0" are performed "simultaneously" it will not necessarily lead to mutual blocking ad infinitum, because both processes will reset their own "c" back to 1 before restarting the entry rites, thereby enabling the other process to catch the opportunity. But our principles force us to reject also this solution, for the refusal to make any assumptions about the speed ratio implies that we have to cater for all speeds, and the last solution admits the speeds to be so carefully adjusted that the processes inspect the other's "c" only in those periods of time that its value is = 0. To make clear that we reject such solutions that only work with some luck, we state our next requirement: "If the two processes are about to enter their critical sections, it must be impossible to devise for them such finite speeds, that the decision which one of the two is the first to enter its critical section is postponed until eternity.".
In passing we note, that the solution just rejected is quite acceptable everyday life. E.g., when two people are talking over the telephone and they are suddenly disconnected, as a rule both try to reestablish the connection. They both dial and if they get the signal "Number Engaged", they put down the receiver and, if not already called, they try "some" seconds later. Of course, this may coincide with the next effort of the other party, but as a rule the connection is reestablished succesfully after very few trials. In our mechanical circumstances, however, we cannot accept this pattern of behaviour: our parties might very well be identical!
Quite a collection of trial solutions have been shown to be incorrect and at some moment people that had played with the problem started to doubt whether it could be solved at all. To the Dutch mathematician Th.J.Dekker the credit is due for the first correct solution. It is, in fact, a mixture of our previous efforts: it uses the "safe sluice" of our last constructions, together with the integer "turn" of the first one, but only to resolve the indeterminateness when neither of the two immediately succeeds. The initial value of "turn" could have been 2 as well.
begin integer c1, c2 turn;
c1:= 1; c2:= 1; turn = 1;
parbegin
process 1: begin A1: c1:= 0;
L1: if c2 = 0 then
begin if turn = 1 then goto L1;
c1:= 1;
B1: if turn = 2 then goto B1;
goto A1
end;
critical section 1;
turn:= 2; c1:= 1;
remainder of cycle 1; goto A1
end;
process 2: begin A2: c2:= 0;
L2: if c1 = 0 then
begin if turn = 2 then goto L2;
c2:= 1;
B2: if turn = 1 then goto B2;
goto A2
end;
critical section 2;
turn:= 1; c2:= 1;
remainder of cycle 2; goto A2
end
parend
end .
We shall now prove the correctness of this solution. Our first observation is that each process only operates on its own "c". As a result process 1 inspects "c2" only while "c1 = 0", it will only enter its critical section provided it finds "c2 = 1"; for process 2 the analogous observation can be made.
In short, we recognize the safe sluice of our last constructions and the solution is safe in the sense that the two processes can never be in their critical sections simultaneously. The second part of the proof has to show that in case of doubt the decision which of the two will be the first to enter cannot be postponed until eternity. Now we should pay some attention to the integer "turn": we note that assignment to this variable only occurs at the end —or, if you wish: as part— of critical sections and therefore we can regard the variable "turn" as a constant during this decision process. Suppose that "turn = 1". Then process 1 can only cycle via Ll, that is with "c1 = 0" and only as long as it finds "c2 = 0". But if "turn = 1" then process 2 can only cycle via B2, but this state implies "c2 = 1", so that process 1 cannot and is bound to enter its critical section. For "turn = 2" the mirrored reasoning applies. As third and final part of the proof we observe that stopping, say, process 1 in "remainder of cycle 1" will not restrict process 2: the relation "c1 = 1" will then hold and process 2 can enter its critical section gaily, quite independent of the current value of "turn". And this completes the proof of the correctness of Dekker's solution. Those readers that fail to appreciate its ingenuity are kindly asked to realize, that for them I have prepared the ground by means of a carefully selected set of rejected constructions.
2.2. The Generalized Mutual Exclusion Problem.
The problem of section 2.1 has a natural generalization: given N cyclic processes, each with a critical section, can we construct them in such a way, that at any moment at most one of them is engaged in its critical section? We assume the same means of intercommunication available, i.e. a set of commonly accessible variables. Furthermore our so1ution has to satisfy the same requirements, that stopping one process well outside its critical section may in no way restrict the freedom of the others, and that if more than one process is about to enter its critical section, it must be impossible to devise for them such finite speeds, that the decision which one of them is the first one to enter its critical section, can be postponed until eternity.
In order to be able to describe the solution in ALGOL 6O, we need the concept of the array. In section 2.1 we had to introduce a "c" for each of the two processes and we did so by declaring
integer array c1, c2 .
Instead of enumerating the quantities, we can declare —under the assumption that "
N" has a well defined positive value—
integer array c[1 : N]
which means, that at one stroke we have introduced
N integers, accessible under the names
c[subscript],
where "
subscript" might take the values 1, 2, .......
N.
The next new ALGOL 60 feature we shall use is the so-called "for clause", which we shall use in the following form:
for j:= 1 step 1 until N do statement S ,
and which enables us to express repetition of "
statement S" quite conveniently. In principle, the
for clause implies that "
statement S" will be executed
N times, with "
j" in succession = 1, = 2, ......, =
N. (We have added "in principle", for via a goto statement as constituent part of
statement S and leading out of it, the repetition can be ended earlier.)
Finally we need the logical operator that in this monograph is denoted by "and". We have met the conditional clause in the form:
if condition then statement .
We shall now meet:
if condition 1 and condition 2 then statement S .
meaning that
statement S will only be executed if "
condition 1" and "
condition 2" are both satisfied. (Once more we should like to stress that this monograph is not an ALGOL 60 programming manual: the above —loose!— explanations of ALGOL 6O have only been introduced to make this monograph as self-contained is possible.)
With the notational aids just sketched we can describe our solution for fixed N as follows.
The overall structure is:
begin integer array b, c[O : N];
integer turn;
for turn:= 0 step 1 until N do
begin b[turn]:= 1 end;
turn:= 0;
parbegin
process 1: begin.....................end;
process 2: begin.....................end;
.
.
.
.
.
.
.
process N: begin.....................end
parend
end .
The first declaration introduces two arrays with N + 1 elements each, the next declaration introduces a single integer "turn". In the following for clause this variable "turn" is used to take on the successive values 1, 2, 3,......, N, so that the two arrays are initialized with all elements = 1. Then "turn" is set = 0 (i.e. none of the processes, numbered from 1 onwards, is privileged). After this the N processes are started simultaneously.
The N processes are all similar. The structure of the i-th process is as follows (1 ≤ i ≤ N) :
process i: begin integer i;
Ai: b[i]:= 0;
Li: if turn ≠ i then
begin c[i]:= 1;
if b[turn] = 1 then turn:= i;
goto Li
end;
c[i]:= 0;
for j:= 1 step 1 until N do
begin if j ≠ i and c[j] = 0 then goto Li end;
critical section i
turn:= 0; c[i]:= 1; b[i]:= 1;
remainder of cycle i; goto Ai
end .
Remark. The description of the N individual processes starts with declaration "integer j". According to the rules of ALGOL 60 this means that each process introduces its own, private integer "j" (a so-called "local quantity").
We leave the proof to the reader. It has to show again:
1) that at any moment at most one of the processes is engaged in its critical section
2) that the decision which of the processes is the first to enter its critical section cannot be postponed until eternity
3) that stopping a process in its "remainder of cycle" has no effect upon the others.
Of these parts, the second one is the most difficult one. (Hint: as soon as one of the processes has performed the assignment "turn:= i", no new processes can decide to assign their number to turn before a critical section has been completed. Mind that two processes can decide "simultaneously" to assign their i-value to turn!)
(Remark, that can be skipped at first reading.) The program just described inspects the value of "b[turn]" where both the array "b" and the integer "turn" are in common store. We have stated that inspecting a single variable is an indivisible action and inspecting "b[turn]" can therefore only mean: inspect the value of "turn", and if this happens to be = 5, well, then inspect "b[5]". Or, in more explicit ALGOL:
process i:= begin integer j, k;
.
.
.
.
k:= turn; if b[k] = 1 then........ ,
implying that by the time that "b[k]" is inspected, "turn" may slready have a value different from the current one of "k".
Without the stated limitations in communicating with the common store, a possible interpretation of "the value of b[turn]" would have been "the value of the element of the array b as indicated by the current value of turn". In so-called uniprogramming —i.e. a single seouential process operating on quantities local to it— the two interpretations are equivalent. In multiprogramming, where other active processes may access and change the same common information, the two interpretations make a great difference: In particular for the reader with extensive experience in uniprogramming this remark has been inserted as an indication of the subtleties of the games we are playing.
2.3. A Linguistic Interlude.
(This section may be skipped at first reading.)
In section 2.2. we described the cooperation of N processes; in the overall structure we used a vertical sequence of dots between the brackets "parbegin" and "parend". This is nothing but a loose formalism, suggesting to the human reader how to compose in our notation a set of N cooperating sequential processes, under the condition that the value of N has been fixed beforehand. It is a suggestion for the construction of 3, 4 or 5071 cooperating processes, it does not give a formal description of N such cooperating processes in which N occurs as a parameter, i.e. it is not a description, valid for amy value of N.
It is the purpose of this section to show that the concept of the so-called "recursive procedure" of ALGOL 60 caters for this. This concept will be sketched briefly.
We have seen, how after "begin" declarations could occur in order to introduce and to name either single varibles (by enumeration of their names) or whole ordered sets af variables (viz. in the array declaration}. With the so-called "procedure declaration" we can define and name a certain action; such an action may then be invoked by using its name as a statement, thereby supplying the parameters, to which the action should be applied.
As an illustration we consider the following ALGOL 6O program:
begin integer a, b;
procedure square(u, v); integer u, v;
begin u:= v * v end;
L: square(a, 3); square(b, a); square(a, b)
end .
In the first line the integer named "a" and "b" are declared. The next line declares the procedure named "square", operating on two parameters, which are specified to be single integers (and not, say, complete arrays). This line is called "the procedure heading". The immediately following statement —the so-called "procedure body"— describes by definition the action named: in the third line —in which the bracket pair "begin....end" is superfluous— it is told that the action of "square" is to assign to the first parameter the square of the value of the second one. Then, labeled "L", comes the first statement. Before its execution the values of both "a" and "b" are undefined, after its execution "a = 9". After the execution of the next statement, the value of "b" is therefore = 81, after the execution of the last statement, the value of "a" is =6561, the value of "b" is still = 81.
In the previous example the procedure mechanism was essentially introduced as a means for abreviation, a means for avoiding to have to write down the "body" three times, although we could have done so quite easily:
begin integer a, b;
L: a:= 3 * 3; b:= a * a; a:= b * b
end .
When the body is much more complicated than in this example, a program along the latter lines tends indeed to be much more lengthy.
This technique of "substituting for the call the appropriate version of the body" is, however, no longer possible as soon as the procedure is a so-called recursive one, i.e. may call itself. It is then, that the procedure really enlarges the expressive power of the programming language.
A simple example might illustrate the recursive procedure. The greatest common divisor of two given natural numbers is
1) if they have the same value equal to this value
2) if they have different values equal to the greatest common divisor of the smallest of the two and their difference.
In other words, if the greatest common divisor is not trivial (first case) the problem is replaced by finding the greatest common divisor of two smaller numbers.
(1n the following program the insertion "
value v, w;" can be skipped by the reader as being irrelevant for our present purposes; it indicates that for the parameters listed the body is only interested in the numerical value of the actual parameter, as supplied by the call.)
begin integer a;
procedure GCD(u, v, w); value v, w; integer u, v, w;
begin if v = w then u:= v
else
begin if v < w then GCD(u, v, w - v)
else GCD(U, v -w, w)
end;
GCD(a, 12, 53)
end .
(In this example the more elaborate form of the conditional statement is used, viz.:
if condition then statement 1 else statement 2 ,
meaning that if "
condition" is satisfied,"
statement 1" will be executed and "
statement 2" will be skipped, and that if "
condition" is not satisfied, "
statement 1" will be skipped and "
statement 2" will be executed.)
The reader is invited to follow the pattern of calls of GCD and to see, how the variable "a" becomes = 3; he is also invited to convince himself of the fact that the (dynamic) pattern of calls depends on the parameters supplied and that the substitution technique —replace call by body— as applied in the previous example would lead to difficulties here.
We shall now write a program to perform a matrix * vector multiplication in which
1) the order of the M scalar * scalar products to be summed is indeed prescribed (the rows of the matrix will be scanned from left to right)
2) the N rows of the matrix can be processed in parallel.
(Where we do not wish to impose the restriction of purely integer values, we have used to declarator "real" instead of the declarator "integer"; furthermore we have introduced an array with two subscripts in a, we hope, obvious manner.)
It is assumed that, upon entry of this block of program, the integers "M" and "N" have positive values.
begin real array matrix[1 : N, 1 : M];
real array vector[l : M];
real array product[l : N];
procedure rowmult(k); value k; integer k;
begin if k > O then
parbegin
begin real s; integer j;
s:= 0;
for j:= 1 step 1 until M do
s:= s + matrix[k, j] * vector[j];
product[k]:= s
end;
rowmult(k -1)
parend
end;
.
.
.
.
.
rowmult(N);
.
.
end
We return to the problem of mutual exclusion in time of critical sections, as introduced in section 2.1 and generalized in section 2.2. This section deals with a more efficient technique for solving this problem; only after having done so, we have adequate means for the description of examples, with which I hope to convince the reader of the rather fundamental importance of the mutual exclusion problem. In other words, I must appeal to the patience of the wondering reader (suffering, as I am, from the sequential nature of human communication!)
3.1. The Need for a More Realistic Solution.
The solution given in section 2.2 is interesting in as far as it shows that the restricted means of communication provided are, from a theoretical point of view, sufficient to solve the problem. From other points of view, which are just as dear to my heart, it is hopelessly inadequate.
To start with, it gives rise to a rather cumbersome description of the individual processes, in which it is all but transparent that the overall behaviour is in accordance with the conceptually so simple requirement of the mutual exclusion. In other words, in some way or another this solution is a tremendous mystification. Let us try to isolate in our minds in which respect this solution represents indeed a mystification, for this investigation could give the clue to improvement.
Let us take the period of time during which one of the processes is in its critical section. We all know, that during that period, no other processes can enter their critical section and that, if they want to do so, they have to wait until the current critical section execution has been completed. For the remainder of that period hardly any activity is required from them: they have to wait anyhow, and as far as we are concerned "they could go to sleep".
Our solution does not reflect this at all: we keep the processes busy setting and inspecting common variables all the time, as if no price has to be paid for this activity. But if our implementation —i.e. the ways in which or the means by which these processes are carried out— is such, that "sleeping" is a less expensive activity than this busy way of waiting, then we are fully justified (now also from an economic point of view) to call our solution misleading.
In present day computers, there are at least two ways in which this active way of waiting can be very expensive. Let me sketch them briefly. These computers have two distinct parts, usually called "the processor" and "the store". The processor is the active part, in which the arithmetic and logical operations are performed, it is "active and small"; in the store, which is "passive and large" resides at any moment the information, which is not processed at that very moment but only kept there for future reference. In the total computational process information is transported from store to processor as soon as it has to play an active role, the information in store can be changed by transportation in the inverse direction.
Such a computer is a very flexible tool for the implementation of sequential processes. Even a computer with only one single processor can be used to implement a number of concurrent sequential processes. From a macroscopic point of view it will seem, as though all these processes are carried out simultaneously, a more closer inspection will reveal, however, that at any "microscopic" moment the processor helps along only one single program, and the overall picture only results, because at well chosen moments the processor will switch over from one process to another. In such an implementation the different processes share the same processor and activity of one of the processes (i.e. a non-zero speed) will imply a zero speed for the others and it is then undesirable, that precious processor time is consumed by processes, which cannot go on anyhow.
Apart from processor sharing, the store sharing could make the unnecessary activity of a waiting process undesirable. Let us assume that inspection of or assignment to a "common variable" implies the access to an information unit —a so-called "word"— in a ferrite core store. Access to a word in a core store takes a finite time and for technical reasons only one word can be accessed at a time. When more than one active process may wish access to words of the same core store, the usual arrangement is that in the case of immanent coincidence, the storage access requests from the different active processes are granted according to a built in priority rule: the lower priority process is automatically held up. (The literature refers to this situation when it describes "a communication channel stealing a memory cycle from the processor.) The result is that frequent inspection of common variables may slow down the process, the local quantities of which are stored in the same core store.
3.2. The Synchronizing Primitives.
The origin of the complications, which lead to such intricate solutions as the one described in section 2.2 is the fact that the indivisible accesses to common variables are always "one-way information traffic": an individual process can either assign a new value or inspect a current value. Such an inspection itself, however, leaves no trace for the other processes and the consequence is that, when a process want to react to the current value of a common variable, its value may be changed by the other processes between the moment of its inspection and the following effectuation of the reaction to it. In other words: the previous set of communication facilities must be regarded as inadequate for the problem at hand and we should lock for better adapted alternatives.
Such an alternative is given by introducing
a) among the common variables special purpose integers, which we shall call "semaphores".
b) among the repertoire of actions, from which the individual processes have to be constructed, two new primitives, which we call the "P-operation" and the "V-operation" respectively. The latter operations always operate upon a semaphore and represent the only way in which the concurrent processes may access the semaphores.
The semaphores are essentially non-negative integers; when only used to solve the mutual exclusion problem, the range of their values will even be restricted to "0" and "1". It is the merit of the Dutch physicist and computer designer Drs.C.S.Scholten to have demonstrated a considerable field of applicability for semaphores that can also take on larger values. When there is a need for distinction, we shall talk about "binary semaphores" and "general semaphores" respectively. The definition of the P- and V-operation that I shall give now, is insensitive to this distinction.
Definition. The V-operation is an operation with one argument, which must be the identification of a semaphore. (If "S1" and "S2" denote semaphores, we can write "V(S1)" and "V(S2)".) Its function is to increase the value of its argument semaphore by 1; this increase is to be regarded as an indivisible operation.
Note, that this last sentence makes "V(S1)" inequivalent to "S1 := S1 + 1".
For suppose, that two processes A and B both contain the statement "V(S1)" and that both should like to perform this statement at a moment when, say, "S1 = 6". Excluding interference with S1 from other processes, A and B will perform their V-operations in an unspecified order —at least: outside our control— and after the completion of the second V-operation the final value of S1 will be = 8. If S1 had not been a semaphore but just an ordinary common integer, and if processes A and B had contained the statement "S1:= S1 + 1" instead of the V-operation on S1, then the following could happen. Process A evaluates "S1 + 1" and computes "7"; before effecting, however, the assignment of this new value, process B has reached the same stage and also evaluates "S1 + 1", computing "7". Thereafter both processes assign the value "7" to S1 and one of the desired increases has been lost. The requirement of the "indivisible operation" is meant to exclude this occurrence, when the V-operation is used.
Definition. The P-operation is an operation with one argument, which must be the identification of a semaphore. (If "S1" and "S2" denote semaphores, we can write "P(S1)" and "P(S2)".) Its function is to decrease the value of its argument semaphore by 1 as soon as the resulting value would be non-negative. The completion of the P-operation —i.e. the decision that this is the appropriate moment to effectuate the decrease and the subsequent decrease itself— is to be regarded as an indivisible operation.
It is the P-operation, which represents the potential delay, viz. when a process initiates a P-operation on a semaphore, that at that moment is = 0, in that case this P-operation cannot be completed until another process has performed a V-operation on the same semaphore and has given it the value "1". At that moment, more than one process may have initiated a P-operation on that very same semaphore. The clause that completion of a P-operation is an indivisible action means that when the semaphore has got the value "1", only one of the initiated P-operations on it is allowed to be completed. Which one, again, is left unspecified, i,e, at least outside our control.
At the present stage of our discussions we shall take the implementability of the P-and V-operations for granted.
3.3. The Synchronizing Primitives Applied to the Mutual Exclusion Problem.
The solution of the N processes, each with a critical section, the executions of which must exclude one another in time (see section 2.2) is now trivial. It can be done with the aid of a single binary semaphore, say "free". The value of "free" equals the number of processes allowed to enter their critical section now, or:
"free = 1" means: none of the processes is engaged in its critical section
"free = 0" means: one of the processes is engaged in its critical section.
The overall structure of the solution becomes:
begin integer free; free:= 1;
parbegin
process 1: begin...............end;
process 2: begin...............end;
.
.
.
.
process N: begin...............end;
parend
end
with the i-th process of the form:
process i: begin
Li: P(free); critical section i; V(free);
remainder of cycle i; goto Li
end
4. The General Semaphore.
4.1. Typical Uses of the General Semaphore.
We consider two processes, which are called the "producer" and the "consumer" respectively. The producer is a cyclic process and each time it goes through its cycle it produces a certain portion of information, that has to be processed by the consumer. The consumer is also a cyclic process and each time it goes through its cycle, it can process the next portion of information, as has been produced by the producer. A simple example is given by a computing process, producing as "portions of information" punched cards images to be punched out by a card punch, which plays the role of the consumer.
The producer-consumer relation implies a one-way communication channel between the two processes, along which the portions of information can be transmitted. We assume the two processes to be connected for this purpose via a buffer with unbounded capacity, i.e. the portions produced need not to be consumed immediately, but they may queue in the buffer. The fact that no upper bound has been given for the capacity of the buffer makes this example slightly unrealistic, but this should not trouble us too much now.
(The origin of the name "buffer" becomes understandable as soon as we investigate the consequences of its absence, viz. when the producer can only offer its next portion after the previous portion has been actually consumed. In the computer - card punch example, we may assume that the card punch can punch cards at a constant speed, say 4 cards per second. Let us assume, that this output speed is well matched with the production speed, i.e. that the computer can perform the card image production process with the same average speed. If the connection between computing process and card punch is unbuffered, then the couple will only work continuously at full speed when the card production process produces a card every quarter of a second. If, however, the nature of the computing process is such, that after one or two seconds vigorous computing it produces 4 to 8 card images in a single burst, then unbuffered connection will result in a period of time, in which the punch will stand idle (for lack of information), followed by a period in which the computing process has to stand idle, because it cannot get rid of the next card image before the preceding one has been actually punched. Such irregularities in production speed, however, can be smoothed out by a buffer of sufficient size and that is, why such a queuing device is called "a buffer".)
In this section we shall not deal with the various techniques of implementing a buffer. It must be able to contain successive portions of information, it must therefore be a suitable storage medium, accessible to both processes. Furthermore, it must not only contain the portions themselves, it must also represent their linear ordering. (In the literature two well-known techniques are described by "cyclic buffering" and "chaining" respectively.) When the producer has prepared its next portion to be added to the buffer, we shall indicate this action simply by "add portion to buffer", without going into further details; similarly, the consumer will "take portion from buffer", where it is understood that it will be the oldest portion, still in the buffer. (Another name of a buffer is a "first-In-first-Out-Memory.)
Omitting in the outermost block any declarations for the buffer, we can now construct the two processes with the aid of a single general semaphore, called "number of queuing portions".
begin integer number of queuing portions;
number of queuing portions:= 0;
parbegin
producer: begin
again 1: produce the next portion;
add portion to buffer;
V(number of queuing portions);
goto again1
end;
consumer: begin
again 2: P(number of queuing portions);
take portion from buffer;
process portion taken;
goto again 2
end
parend
end
The first line of the producer represents the coding of the process which forms the next portion of information; it can be conceived —it has a meaning— quite independent of the buffer for which this portion is intended; when it has been executed the next portion has been succesfully completed, the completion of its construction can no longer be dependent on other (unmentioned) conditions. The second line of coding represents the actions, which define the finished portions as the next one in the buffer; after its execution the new portion has been added completely to the buffer, apart from the fact that the consumer does not know it yet. The V-operation finally confirms its presence, i.e. signals it to the consumer. Note, that it is absolutely essential, that the V-operation is preceded by the complete addition of the portion. About the structure of the consumer analogous remarks can be made.
Particularly in the case of buffer implementation by means of chaining it is not unusual that the operations "add portion to buffer" and "take portion from buffer" —operating as they are on the same clerical status information of the buffer— could interfere with each other in a most undesirable fashion, unless we see to it, that they exclude each other in time. This can be catered for by a binary semaphore, called "buffer manipulation", the values of which mean:
= 0 : either adding to or taking from the buffer is taking place
= 1 : neither adding to nor taking from the buffer is taking place.
The program is as follows:
begin integer number of queuing portions, buffer manipulation;
number of queuing portions:= 0;
buffer manipulation:= 1;
parbegin
producer: begin
again 1: produce next portion;
P(buffer manipulation) ;
add portion to buffer;
V(buffer manipulation);
V(number of queuing portions);
goto again 1
end;
consumer: begin
again 2: P(number of queuing portions);
P(buffer manipulation);
take portion from buffer;
V(buffer manipulation);
process portion taken;
goto again 2
end
parend
end
The reader is requested to convince himself that
a) the order of the two V-operations in the producer is immaterial
b) the order of the two P-operations in the consumer is essential.
Remark. The presence of the binary semaphore "buffer manipulation" has another consequence. We have given the program for one producer and one consumer, but now the extension to more producers and/or more consumers is straightforward: the same semaphore sees to it that two or more additions of new portions will never get mixed up and the same applies to two or more takings of a portion by different consumers. The reader is requested to verify that the order of the two V-operations in the producer is still immaterial.
4.2. The Superfluity of the General Semaphore.
In this section we shall show the superfluity of the general semaphore and we shall do so by rewriting the last program of the previous section, using binary semaphores only. (Intentionally I have written "we shall show" and not "we shall prove the superfluity". We do not have at our disposal the mathematical apparatus that would be needed to give such a proof and I do not feel inclined to develop such mathematical apparatus now. Nevertheless I hope that my show will be convincing!) We shall first give a solution and postpone the discussion till afterwards.
begin integer numqueupor, buffer manipulation, consumer delay;
numqueupor:= 0; buffer manipulation:= 1; consumer delay:= 0;
parbegin
producer: begin
again 1: produce next portion;
P(buffer manipulation);
add portion to buffer:
numqueupor:= numqueupor + 1;
if numqueupor = 1 then V(consumer delay);
V(buffer manipulation);
goto again 1
end;
consumer: begin integer oldnumqueupor;
wait: P(consumer delay);
go on: P(buffer manipulation);
take portion from buffer;
numqueupor:= numqueupor -1;
oldnumqueupor:= numquepor;
V(buffer manipulation) ;
process portion taken;
if oldnumqueupor = 0 then goto wait else goto go on
end
parend
end .
Relevant in the dynamic behaviour of this program are the periods of time during which the buffer is empty. (As long as the buffer is not empty, the consumer can go on happily at its maximum speed.) Such a period can only be initiated by the consumer (by taking the last portion present from the buffer), it can only be terminated by the producer (by adding a portion to an empty buffer). These two events can be detected unambiguously, thanks to the binary semaphore "buffer manipulation", that guarantees the mutual exclusion necessary for this detection. Each such period is accompanied by a P- and a V-operation on the new binary semaphore "consumer delay". Finally we draw attention to the local variable "oldnumqueupor" of the consumer: its value is set during the taking of the portion and fixes, whether it was the last portion then present. (The more expert ALGOL readers will be aware that we only need to store a single bit of information, viz. whether the decrease of numqueupor resulted in a value = 0; we could have used a local variable of type Boolean for this purpose.) When the consumer decides to go to "wait" i.e. finds "oldnumqueupor = 0", at that moment "numqueupor" itself could already be greater than zero again!
In the previous program the relevant occurrence was the period with empty buffer. One can remark that emptiness is, in itself, rather irrelevant: it only matters, when the consumer should like to take a next portion, which is still absent. We shall program this version as well. In its dynamic behaviour we may expect less P- and V-operations on "consumer delay", viz. not when the buffer has been empty for a short while, but is filled again in time to make delay of the consumer unnecessary. Again we shall first give the program and then its discussion.
begin integer numqueupor, buffer manipulation, consumer delay;
numqueupor:= 0; buffer manipulation:= 1; consumer delay:= 0;
parbegin
producer: begin
again 1: produce next portion;
P(buffer manipulation);
add portion to buffer;
numqueupor:= numqueupor + 1;
if numqueupor = 0 then
begin V(buffer manipulation);
V( consumer delay) end
else
V(buffer manipulation);
goto again 1
end;
consumer: begin
again 2: P(buffer manipulation);
numqueupor:= numnqueupor -1;
if numqueupor = -1 then
begin V(buffer manipulation);
P(consumer delay);
P(buffer manipulation) end;
take portion from buffer;
V(buffer manipulation);
process portion taken;
goto again 2
end
parend
end
Again, the semaphore "buffer manipulation" caters for the mutual exclusion of critical sections. The last six lines of the producer could have been formulated as follows:
if numqueupor = 0 then V(consumer delay);
V(buffer manipulation); goto again 1
In not doing so I have followed a personal taste, viz. to avoid P- and V-operations within critical sections; a personal taste to which the reader should not pay too much attention.
The range of possible values of "numqueupor" has been extended with the value "-1", meaning (outside critical section execution) "the buffer is not only empty, but its emptyness has already been detected by the consumer, which has decided to wait". This fact can be detected by the producer when, after the addition of one, "numqueupor = 0" holds.
Note how, in the case of "numqueupor = -1" the critical section of the consumer is dynamically broken into two parts: this is most essential, for otherwise the producer would never get the opportunity to add the portion that is already so much wanted by the consumer.
(The program just described is known as "The Sleeping Barber". There is a barbershop with a separate waiting room. The waiting room has an entry and next to it an exit to the room with the barber's chair, entry and exit sharing the same sliding door which always closes one of them; furthermore the entry is so small that only one customer can enter it at a time, thus fixing their order of entry. The mutual exclusions are thus guaranteed.
 Fig. 1. x < y
Fig. 1. x < y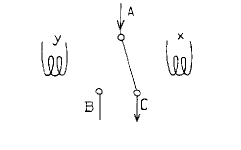 Fig. 2. y < x
Fig. 2. y < x