NOTE: This transcription was contributed by Martin P.M. van der Burgt, who has devised a process for producing transcripts automatically. Although its markup is incomplete, we believe it serves a useful purpose by virtue of its searchability and its accessibility to text-reading software. It will be replaced by a fully marked-up version when time permits. —HR
About polygons in Detroit.
After my trip from Nuenen to Detroit I suffered, as usual, from the
six-hour time shift, and, in bed but hopelessly awake, I posed myself the
problem, what shape a polygon with sides of given lengths would take if the
enclosed area had to be of maximum value. With the polygon built from rigid
sides, in their endpoints flexibly joined to their two neighbours, the shape
enclosing the maximum area is stable when a constant outward pressure p is
exerted on all sides; hence the resulting outward force on each side is
compensated by the forces of reaction exerted upon it by its two neighbours.
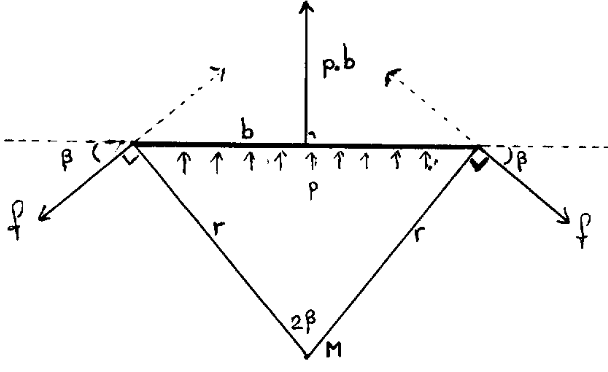
The outward force resulting from the pressure p exerted on a side of length b equals p.b , applied to its midpoint in a direction orthogonal to it. The stability of the side requires that the parallel components of the two reaction forces cancel, and that their orthogonal components be p.b/2 . Hence the two reaction forces have the same value, f say, and make the same angle, β say, with the side, the four quantities being related by
| p.b = 2.f.sin(β) |
In each endpoint we now draw a line orthogonal to the force of reaction, and call the point where these two lines meet M . Because the two lines meet at an angle 2.β , and the point M lies at the same distance, r say, from the two endpoints, we have
| b = 2.r.sin(β) . |
| r = f/p . | (1) |
Because the interchange of two neighbouring sides leaves the area enclosed and the radius of the circumscribed circle invariant, we conclude that the maximum area enclosed and the radius of the circumscribed circle only depend on the lengths of the sides, but not on the order in which these lengths occur along the circumference.
10 December 1978
| Plataanstraat 5 | prof.dr.Edsger W.Dijkstra |
| 5671 AL Nuenen | Burroughs Research Fellow |
| The Netherlands |
Transcribed by Martin P.M. van der Burgt
Last revision