NOTE: This transcription was contributed by Martin P.M. van der Burgt. Although its markup is incomplete, we believe it serves a useful purpose by virtue of its searchability and its accessibility to text-reading software. It will be replaced by a fully marked-up version when time permits. —HR
Image reconstruction in two-dimensional tomography.
In two-dimensional tomography the patient is
placed in a ring. In its plane the ring can rotate
around its centre. In one point of the ring an
X-ray source is placed that, when pulsed, emits
a fan of X-rays towards a sequence of detectors
placed along the ring opposite to the source:
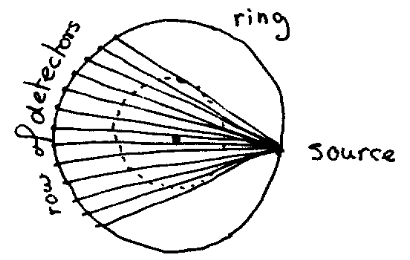
During "the taking of a picture" the ring makes a full rotation, the source is pulsed regularly, and for each pulse the intensity of the ray reaching each of the detectors is recorded. Provided the patient is placed inside the dotted circle —the largest circle always covered by the fan— from the recorded information one should reconstruct the distribution of the absorption density in the plane of the patient that has been traversed in many directions by the X-rays of the fan.
Note 1. This reconstruction gets blurred if, during "the taking of the picture" the patient moves. It is therefore essential that a full rotation of the ring does not take more than a few seconds. (End of Note 1.)
Note 2. It is essential that in each point of the picture to be reconstructed, the rays that have traversed it are equi-angular distributed. that is why the picture has to be confined to the interior of the dotted circle, and furthermore
| a) | the angle between the rays from source to two successive detectors in 2π/N (integer N, large) |
| b) | the rotation of the ring between two successive pulsea is 2π / N' (integer N', large and a factor of N) |
(For the measuring apparatus shown to me, the number of detectors —i.e. the number of rays in the fan— was 288; N was 2400, and N' was 600. N=2520 and N'=630 has some attraction for the machine to be described below, because 2520 is the smallest number divisible by the numbers 2 through 10.)
The number of measured values per rotation
equals N' * K if K equals the number of detectors.
Each measured value corresponds to a particular
ray traversing the specimen being probed, but
contributes in the reconstruction proces to each
point of the image. This contribution to the
absorption density in the image is constant along
lines parallel to the ray that corresponds to the
value measured, more particular
1) it is proportional to the value measured
2) positive along the ray
3) negative everywhere and proportional to 1 / r2 if
r = the distance between the ray and the line
parallel to it, along which we are considering
the contribution.
Note 3. For the justification of the positive contribution along the ray and a negative contribution elsewhere I must refer to the public literature. (End of note 3.)
Note 4. For each point of the image the N' * K contrubutions to the total absorption density must be accumulated. As normal storage tubes can only "add" but not "subtract", the presence of positive and negative values to be accumulated calls for numerical techniques. (End of Note 4.)
Note 5. The specimen is probed by K * N' rays in n different directions. For each set of K * N' / N rays in a particular direction the combined contribution to the absorbtion density is constant along lines parallel to that direction. If so desired —primarily at the expenses of storage because the measurements corresponding to such a set of rays must be collected from as many successive flashes of the X-ray source— this combination can be used to reduce the computational work of accumulating contributions in each point of the image by a factor K * N' / N.
In order to propagate the (single or combined) contribution in a given direction and in each stipe the value to be contributed is taken constant —say the average — . The stripes —not necessarily of the same width— must be small enough to represent the values to be with enough accuracy. The introduction of the stripes represents the discretization of the addition to the assumulated absorption density.
Furthermore the image is subdivided into fields, and in each field the absorption density is regarded constant. Fields must be chosen small enough to give the required resolution in the picture of the absorbtion density to be displayed,
Each stripe contributes only to the fields it covers, totally or partially: it contributes to each such field its function value multiplied by the fraction of the field covered by the stripe. If fields are so small that each field is covered by at most two stripes this requires at most one multiplication per field for each propagation.
The above is standard and should be publicly known.
⇒ The first part off the invention is to choose the fields in concentric rings —not necessarily of the same width—, in each ring all fields are of equal size and their total number in a ring being N/k for some suitable value of k.
In the outermost ring k=3 seems to give fields that are small enough. As the rings get smaller, fields become unnecessary small and we can switch to rings subdivided into N/4 fields. Still closer to the centre we can switch to N/5 etc. (Because 2400 has no factor 7, N=2520 has some —at least theoretical— advantage; 2400 has no factor 9 either.)
Is this choice of fields that facilitates the propagation of contributions to the absorbtion density in N different directions.
⇒ The second part of the invention is to build a machine of as many "elements" as there are fields in the picture; at each moment each element takes care of one field although not necessarily always the same field. The elements are such that at each moment they represent the image in one of its N possible orientations with respect to the stripes.
⇒ The third part of the invention is to interconnect and construct elements in such a way that with respect the stripes the image can be rotated (both ways and repeatedly) over 2π/N, but to do so without loss of information.
The elements in a ring with N/k fields take care of a field in a k "successive" positions, where "successive" is meant in the sense that the transition from one position to the next amounts to an image rotation of 2π/N. Each element has a counter c satisfying 0 ≤ c < k , at each moment the c-values of the elements of a ring have the same value. A clockwise rotation over 2π/N amounts in each ring to c:= (c+1) mod k, an anti-clockwise rotation over 2π/N amounts to c:= (c-1) mod k. Furthermore, when in the clockwise rotation c:= (c+1) mod k leads to c = 0, each element transmits the absorption density to its clockwise neighbour in the ring, and when in the anti-clockwise rotation c is initially = 0, each element transmits the absorption density to its anti-clockwise neighbour in the ring; they continue in both cases to work with the absorption density received.
For this purpose the elements taking care of the fields of a ring are cyclically ordered as the corresponding fields, and each element only needs to be connected to its two immediate neighbours in that order. These are the only inter-element connections needed.
⇒ The fourth part of the invention is to exploit the possibility of rotating the image through the elements for reducing the number of element - stripe connections. Each element —only taking care of fields in k successive positions— need only to be connected to to those stripes that cover (partially) the field in one of the k positions. Bounded by 0 and 1 the fraction of the field covered by a stripe can be taken as a linear function of c. When, compared to the width of the stripes, the fields are so small that the area covered by k successive field positions —this is equal to (2 - 1/k) * the area of the field— is covered by two stripes, no element needs to be connected to more than two stripes.
Via how many channels an element receives stripe values is left to the implementation: presumably a single channel suffices, carrying the values corresponding to the (possibly) covering stripes in some order.
* *
*
Discussion.
Besides the freedom of the width of the stripes —no matter how they are chosen, each stripe gives rise to one constant for each detector—, the freedom of the width of the concentric rings and the value of k, the fields in concentric rings with the same value of k can be staggered. This could remove "radii" —or the appearance thereof— in the picture.
I nowhere said that we need a microcomputer —chip— per element. We have of the order of magnitude of 50.000 elements. If the combination of measurements corresponding to parallel rays is affected we need to accommodate N propagations in about 4 seconds, i.e. 1.6 msec per propagation; if each chip takes care of 16 elements, we have of the order of magnitude 3000 to 4000 chips with about 100 μsec available per propagation per element. If we combine "geometrically near" fields to have their elements taken care of by a single chip —for example 4 consecutive fields from 4 consecutive rings— what has been said about inter-element connectivity can be said with equal force about inter-chip connectivity, and the number of stripes that need to communicate with each chip also remains as limited as can be —goes from 2 till 5 by way of speaking—.
If a chip takes care of a cluster of fields of at most k successive rings with N/k fields, all these rings can be given different c-values, so that each rotation over 2π/N gives rise to at most one absorption density value being transmitted from one chip to the next chip.
In the final machine chips taking care of (a set of rings) need not be arranged in a circle!

| may be flattened as |

|
* *
*
I don't know how you do patent this. It is a special purpose machine consisting of a very special —taylored, I might say— connection pattern between a few thousand, presumably programmed, components. For production and flexibility reasons these components could be "hardwired" equal, with a loading procedure from a magnetic tape containing all the constants computed by a big machine.
20 March 1979 (24.55)
| NUENEN | Edsger W. Dijkstra. |
att. mr. Peterson, K.R.
Transcribed by Martin P.M. van der Burgt
Last revision