A computing scientist's approach to a once-deep theorem of Sylvester's
Well, actually it wasn't Sylvester's theorem, it was only his conjecture —dating from the year 1893—, and it remained so for more than 40 years until T. Gallai (alias Grunwald) "finally succeeded, using a rather complicated argument" [Coxeter]. We shall derive (essentially) the simple argument of L.M. Kelly (1948).
Theorem Consider a finite number of distinct points in the real Euclidean plane; these points are collinear or there exists a straight line through exactly 2 of them.
To see that this is truly a geometric theorem and not a combinatorial one, we slightly rephrase the setting. Let us assume for a moment that collinearity of points in the Euclidean plane is fully captured by
(i) any pair of points are collinear, and if two collinear triples have two points in common, their four points are collinear.
Let us rephrase this: replace "points" by "people", "lines" by "clubs" and "collinear" by "club-sharing" (i.e., belonging to the one and the same club). Club membership is postulated to satisfy the analogue of (i):
(ii) any pair of people is club-sharing, and if two club-sharing triples have two people in common, their four people are club sharing.
The analogue of Sylvester's theorem would state for a finite population: all people belong to one and the same club or there exists a club with exactly 2 members. Its falsity is shown by the following counterexample of 7 people —numbered from 0 through 6— with the following 7 clubs: {013}, {124}, {235}, {346}, {450}, {561}, and {602}. Postulate (ii) is satisfied because each of the 21 pairs of people occurs in exactly 1 club. Thus we have established that Sylvester's theorem is truly a geometrical one; let us now try to prove it.
Being computing scientists, we love constructive arguments, i.e. we like to show that something exists by designing an algorithm that computes such a thing. We therefore propose to design an algorithm that computes a line that passes through exactly 2 of the points from a given finite, non-collinear set of distinct points. (Legenda: from here on we no longer repeat that the points are distinct, nor that they belong to the given, non-collinear set.)
More precisely, we have to design an algorithm that operates on a variable q of type: line and that establishes the post-condition R, given by
R : q passes through exactly 2 of the points.
The simplest idea is to initialize q by the line through 2 arbitrary points. (This is always possible because, the given set being non-collinear, there are at least 3 points.) If q goes through 3 or more points, it has to be changed, otherwise it can be accepted as final value. That is, with invariant P given by
P : q passes through ≥ 2 points
we propose as first approximation of our algorithm
establish P by initialization of q ; do q passes through ≥ 3 points → change q under invariance of P od
Because
P ∧ ¬ (q passes through ≥ 3 points) ⇒ R
we are done when the algorithm terminates.
Our remaining task is to ensure that it does terminate. To that end we have to exploit the finiteness of the given set and its non-collinearity. Because the exploitation of finiteness is absolutely standard, we first focus our attention on what we can conclude from the non-collinearity. From the latter we can draw only one conclusion in connection with q, viz. the existence of a point through which q does not pass. That is, we propose to introduce a variable E of type: point, and to strengthen P to P1
P1: q passes through ≥ 2 points ∧ q does not pass through E.
The new approximation of our algorithm is
establish P1 by initialization of q and E
; do q passes through ≥ 3 points →
{?} change q under invariance of P1
od
(Ignore for a moment the assertion "{?}"; the important thing to realize is that with the feasibility of maintaining the stronger P1, the non-collinearity of the given set has been exhausted.)
In the current stage of program design, our only option is a further refinement of the as yet rather nondeterministic
(0) "change q and E under the invariance of P1"
Because we may have to reduce its nondeterminism lest the algorithm fails to terminate, let us investigate its freedom: what precondition {?} can we guarantee? We know of the existence of 4 points, viz. E and the three points on the current q. Because the new q has to pass through ≥ 2 points and has to differ from the old q, the new q passes through the old E and one of the 3 points on the old q; in each case, one of the remaining 2 points on the old q has to be chosen as the new E. In summary: for the new pair (q, E ) we have 6 possibilities.
For the termination argument we need a variant function of the pair (q, E ); because the number of points is finite, the number of pairs (q, E ) satisfying P1 is finite, and any function of the pair (q, E ) that decreases at each change will do.
What is the simplest function of a line and a point (not on that line) that we can think of? The Euclidean distance between the two!
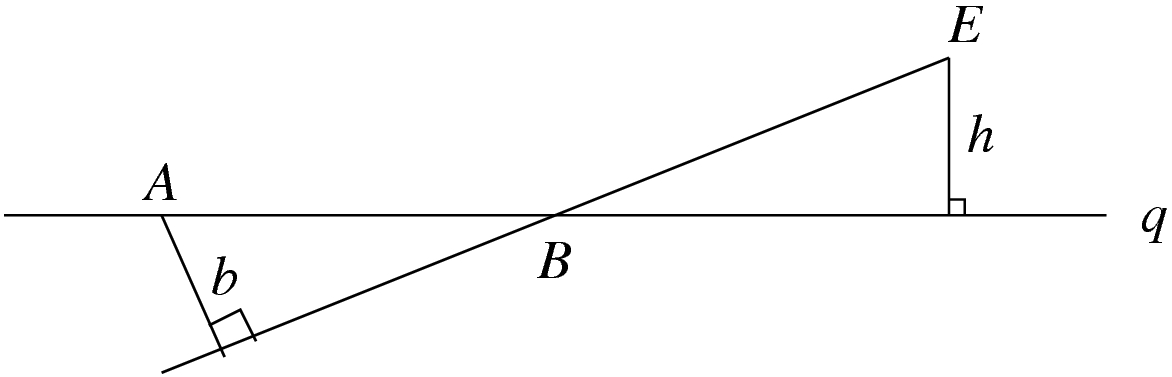
Let us investigate whether we can refine (0) so as to decrease the distance between q and E. Let us name the three points on the old q: A, B, C, so that A becomes the new E. With that convention, the refinement of (0) that decreases the distance of the pair (q, E ) as much as possible is
(1) q, E := of BE and CE the nearest to A, A.
Finally we derive a condition on A as our choice for the new E from the requirement that the variant function decreases. With
h = distance between E and q
b = distance between A and BE
c = distance between A and CE
the required decrease of the variant function is expressed by
(2) b min c < h
In order to derive (2), we proceed as follows
b min c < h
= { definition of min }
b<h ∨ c<h
= { similar triangles, see figure }
AB<EB ∨ AC<EC
⇐ { monotonicity of + } (See Note)
AB+AC < EB+EC
⇐ { P1 ⇒ BC < EB+EC, i.e. the strict triangle inequality } (See Note)
AB+AC ≤ BC
= { AB+AC ≤ BC, i.e. trianglular inequality }
AB+AC = BC
= { AB, AC and BC denote unsigned lengths }
on q, A lies between B and C.
Hence, with for A the point between the two others, (1) does the job. And this concludes our proof of Sylvester's theorem.
Note Since steps that express equivalence don't destroy information, the others need some more justification. We all know the monotonicity of ≥ , i.e. no one doubts
x≥x' ∧ y≥y' ⇒ x+y ≥ x'+y';
its counterpositive yields the equivalent
x<x' ∨ y<y' ⇐ x+y < x'+y'
and that is what we used.
To justify the next step, a second look at our demonstrandum (2) suffices: since it is impossible to demonstrate (2) for h=0, we have to use once more that q does not pass through E. Since E occurs in this calculation in the combinations EB and EC, we translate this into the non-degeneracy of triangle BEC. The step eliminates E for the rest of the calculation. (End of Note.)
For the sake of completeness we point out that, after the choice of the variant function, we have made two silent choices. We have chosen —as usual— to decrease the variant function; because of the finiteness, successfully increasing it would also have yielded a valid termination argument. With a huge h and ABC close together, however, the distance between E and q cannot be increased, which settles this silent choice. Moreover, we could have grouped our 6 cases differently, viz. by common new q instead of by common new E. We could have said "Let us name the three points so that AE becomes the new q" and instead of (1) we would have come up with
q,E := AE, of B and C the nearest to AE.
It does not work.