On covering a figure with diamonds
In the American Mathematical Monthly (May 1989, pp.429–431), under the title “The Problem of the Calissons”, Guy David and Carlos Tomei present the theorem given below. Before formulating the theorem, we introduce some terminology.
We consider a regular triangularization of the Euclidean plane, the grid lines of which cut up the plane into equilateral triangles with sides of length 1; in the following, “triangle” refers to such an equilateral triangle. Note that triangles occur in two orientations and that we can colour them accordingly, e.g.

A pair of differently coloured triangles that share a side is referred to a “diamond”, and a moment’s reflection tells us that each diamond has one of three possible orientations, viz.
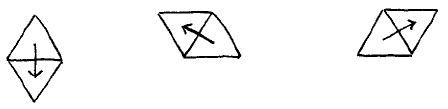
A “figure” is a finite set of triangles; a “covering”of a figure is a partitioning of the figure’s triangles into diamonds.
The theorem presented by David and Tomei states that in any covering of a regular hexagon with sides of length n (and comprising 6n² triangles), the diamonds occur in the three orientations in equal numbers.
* * *
Because of the rotational symmetry of the hexagon, the above theorem is an immediate consequence of the following one.
Theorem Consider a figure that admits one or more coverings. Each covering yields a triple of frequencies, each counting the diamonds in one of the orientations. All coverings of the figure considered yield the same triple.
With the aid of some colleagues, we found for the latter theorem an argument so sweet that it was submitted to the AMM and accepted for publication. But then I withdrew it when I learned that undergraduate students at the Pontifícia Universidade Católica do Rio de Janeiro knew the following, much shorter proof.
Consider a covering of the figure. Draw in each diamond a vector from the centre of its white triangle to the centre of its black triangle. Denote the three possible vectors by ξ,η,ζ and the triple of their frequencies by x,y,z . By adding all these vectors in the covering of the figure, we get the vector equation
x∙ξ + y∙η + z∙ζ = (the sum of the black centres) – (the sum of the white centres) .
Moreover we have the scalar equation
x + y + z = half the number of triangles in the figure .
These three independent linear equations in x,y,z have right-hand sides wholly determined by the figure, and hence determine the triple of frequencies independent of the covering.
I thought the above, as yet anonymous argument too beautiful not to be publicly recorded.
Austin, 9 December 1989
prof.dr. Edsger W.Dijkstra
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712-1188
USA.