For Bill Walker a sequel to EWD1099
When I showed to Bill Walker my arguments for demonstrating [R ] in the form [¬R ⇒ R ], he said he would like to see an example. My first remark is that a proof by case analysis can serve as example:
[¬Q ⇒ R ] ∧ [Q ⇒ R ] , hence [R ] ;
taking the contrapositive of the first conjunct, and appealing to the transitivity of implication we get the scheme
[¬R ⇒ Q ] ∧ [Q ⇒ R ] , hence [¬R ⇒ R ] .
* *
*
Here is my example for Bill Walker (see EWD1053). Our universe of discourse is a Euclidean plane in which each point is red, white, or blue. Our proof obligation R is
R : there exists a monochrome pair of points with mutual distance 1.
The intermediate predicate Q is
Q : all pairs of points with mutual distance √3 are monochrome.
In the following pictorial hints, drawn lines connect points, distance 1 apart, and dotted lines points at distance √3.
Note Monochrome means "of equal colour". The only significance of equality is that it is preserved in function application (Leibniz). The only function defined on our colour domain is equality, and applying Leibniz's principle to it yields that equality is transitive. And that is why an appeal to the transitivity of = has to occur in this proof. (End of Note.)
⇒ { 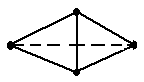 , pigeon-hole principle }
, pigeon-hole principle }
Q
⇒ { , transitivity of equality }
, transitivity of equality }
R .
Nuenen, 10 July 1991
prof.dr. Edsger W.Dijkstra
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712–1188
USA
transcribed by Guy Haworth
revised