The checkers problem told to me by M.O.Rabin
Last week, during the annual seminar at the University of Newcastle-upon-Tyne, Michael O. Rabin told me the following problem.
Consider an infinite checkers board, of which the columns and rows are identified by the integer coordinates x and y respectively. Initially, there is a piece on each square whose coordinates satisfy (even.x ≡ even.y) ∧ y ≤ 0. Pieces can be moved "upwards" by the usual "capturing moves": from 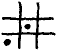 to
to 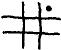 and from
and from 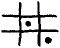 to
to 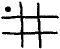 . The question posed is whether there is an upper bound on the y-coordinates of the squares that may be occupied.
. The question posed is whether there is an upper bound on the y-coordinates of the squares that may be occupied.
* * *
Because the question asked is about y-coordinates, we abstract for a moment from the x-coordinate. The two original moves then become one and the same move: from  to
to  . In order to capture that a high piece is created from ("is as good as", "corresponds to") its two successors —those who know him see Fibonacci lurking around the corner!— , we give a piece (on a square) at height y a weight φy with φ the positive root of φ2 = φ + 1 . The equation is chosen so that the weight of the new piece equals the weight of the two pieces it replaces, i.e. a move is neutral as far as total weight is concerned. By restricting ourselves to the positive root, we keep all weights positive, i.e. total weight a monotonic function of the number of pieces involved. Solving the equation yields
. In order to capture that a high piece is created from ("is as good as", "corresponds to") its two successors —those who know him see Fibonacci lurking around the corner!— , we give a piece (on a square) at height y a weight φy with φ the positive root of φ2 = φ + 1 . The equation is chosen so that the weight of the new piece equals the weight of the two pieces it replaces, i.e. a move is neutral as far as total weight is concerned. By restricting ourselves to the positive root, we keep all weights positive, i.e. total weight a monotonic function of the number of pieces involved. Solving the equation yields
φ = (1 + √5)/2 . |
The fact that a move is neutral as far as total weight is concerned, means that the creation of a piece at height Y (with Y>0) uses from the original configuration a set of pieces with total weight φY. This "target weight", being φY and φ being positive, grows exponentially with Y. We shall next observe that, in view of the shape of the two moves —x re-enters the picture— , the original pieces involved in the creation of a piece at height Y come from a restricted area. Calling their total weight the "available weight", we shall show that the latter grows linearly with Y. Hence, the condition
target weight ≤ available weight
imposes an upper bound on Y: the answer to the question posed is "Yes".
In order to establish the available weight we observe the moves for small values of Y.
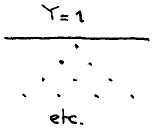
Y=1 requires a single move, say  .
.
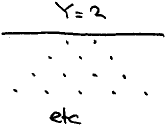
Y=2 requires two moves, say  ,
,
the one thin dot above the
line indicating a square
that has been temporarily
occupied.
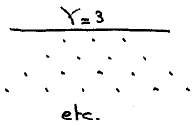
Y=3 requires two moves more. 
For the restricted areas from which the original pieces have to be recruited we take infinite (truncated) triangles
 |  |  |
For Y=1 , the available weight (∑n: n≥0: (n+1)∗φ-n) is finite, and so is the increment (∑n: a≥0: φ-n). Summing the sequences one finds for the available weight
4 + 2√5 + Y∗(3 + √5)
2
The smallest value for Y such that the target weight φY exceeds the available weight is 7 : then the target weight equals (29+13√5)/2, the available weight is only (25+9√5)/2 .
For Y=6, the target weight (18+8√5)/2 is less than the available weight (22+8√5)/2 , but this does not justify the conclusion that Y=6 is attainable. Y=6 can be achieved, but the only way of showing this that I know of is showing a game that does the job. The required game turns out to have 53 moves, which makes finding it and reporting it somewhat of a challenge. I could convince myself that Y=6 could be reached only
(i) after having realized that the constraint of at most 1 piece per square is inessential and can be stopped
(ii) after having decided to play the game backwards
Below, we show successive stages of the backwards game: in the centre the configuration of the pieces, to the left the y-coordinates of the rows in question and —by way of check— to the right for each row the total number of pieces in it.
6 1 1 5 1 1 4 1 1 4 1 1 2 3 1 1 3 1 1 1 3 2 1 1 2 2 1 2 1 1 5 1 1 1 1 3 1 1 1 2 2 2 8 0 1 1 1 1 1 5 0 2 2 2 2 3 2 13 -1 1 1 2 1 1 1 1 8 0 1 1 1 1 1 1 6 -1 2 2 3 2 2 2 2 15 -2 1 1 1 1 1 1 1 7 0 1 1 1 1 1 1 6 -1 1 1 1 1 1 1 1 7 -2 2 2 2 2 2 1 2 2 15 -3 1 1 1 1 1 1 1 1 8 and now not repeating all the constant rows -1 1 1 1 1 1 1 1 7 -2 1 1 1 1 1 1 1 1 8 -3 2 1 2 1 2 2 1 2 2 15 -4 1 1 1 1 1 1 1 7 -2 1 1 1 1 1 1 1 1 8 -3 1 1 1 1 1 1 1 1 1 9 -4 2 1 1 2 2 1 1 1 2 13 -5 1 1 1 1 1 1 6 -3 1 1 1 1 1 1 1 1 1 9 -4 1 0 1 1 1 1 1 1 1 1 9 -5 1 1 1 2 1 1 1 1 1 10 -6 1 1 1 1 4 -4 1 0 1 1 1 1 1 1 1 1 9 -5 1 1 1 1 1 1 1 1 1 9 -6 1 1 1 1 1 5 -7 1 1
There may exist a game of 51 moves, but I am not interested in that optimization. The above is already more elaborate than I had hoped.
Austin, 20 September 1992