On arcs and angles
For the sake of comparison I shall give two presentations of (almost) the same theory. It is about a little corner of Euclidean geometry, relating the size of angles to the length of arcs of circles. When measuring the length of such arcs, we take the radius of the circle as our unit of length.
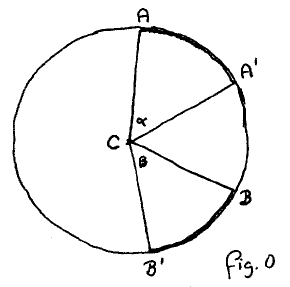
I shall first present the theory as I remember it from half a century ago.
Lemma 0 was about angles with their vertex at C (= the centre of the circle) and states that in fig. 0
|
or “equal angles, equal arcs”. This theorem was proved via the congruence △ACA´ ≌ △BCB´, and allows us to introduce the radian as unit of angle size: the size of an angle with vertex at C equals the length of the corresponding arc. This last formulation I consider a rephrasing of Lemma 0 :
|
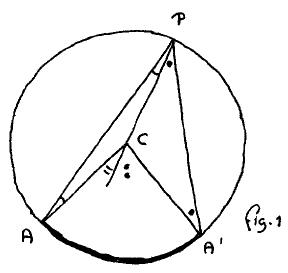
Lemma 1 was concerned with the size of ∠APA´ with all three points on the circle: it states
|
The proof identifies two isosceles triangles and then establishes ∠ACA´ = 2 ∗ ∠APA´ ; with Lemma 0, Lemma 1 then follows.
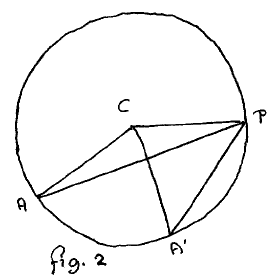
The mathematics is already getting slightly unattractive, for the argument based on fig. 1 is not immediately applicable to fig. 2. This can be remedied by giving the analogous argument for fig. 2, but we are then still left with the question of whether fig. 1 and fig. 2 cover all cases.
Lemma 2 deals with the case that the vertex is an arbitrary point P inside or on the circle, as in fig. 3: it states
|
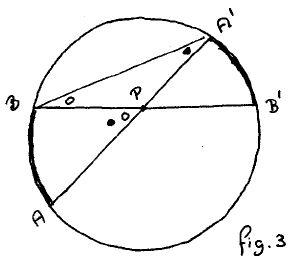
The proof is by observing
∠APB = ∠B´BA´ + ∠BA´A
and then applying Lemma 1 twice. Here we didn’t struggle with the position of the circle’s centre, but do face the question of P lying outside the circle:
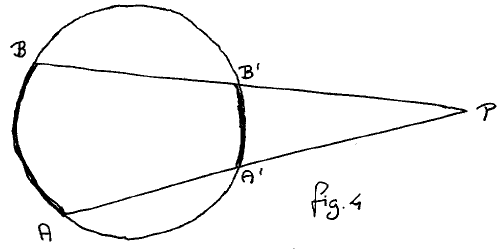
My highschool textbook solved this problem by introducing a new theorem —Lemma 3— stating that in fig. 4
|
and proving this theorem afresh (again by drawing the auxiliary line A´B).
The above is not too satisfactory for a variety of reasons.
- Lemmata 0 and 1 are special cases of Lemma 2.
- Lemmata 2 and 3 ask to be merged into a single lemma, e.g. by the introduction of something like a negative arc.
- There is no uniform, nonpictorial definition of which arcs have to be added or subtracted to yield which angle.
A closer inspection tells us that the notion of an angle, as used thus far, is probably too crude for our purposes.
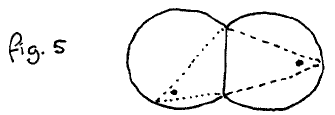
For instance, the traditional definition of a circle is the locus of all points at given distance from a given point; Lemma 2 invited the alternative definition as the locus of points from where a given line segment is seen under the same angle or something like that, but our definition should reject fig. 5 as our circle thus defined! (The vertical line is the segment in question.)
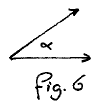
Our notion of “angle” as used thus far is based on the notion of the angle between two rays, both starting at the vertex, as in fig. 6. It is a symmetric function of the two rays that delineate it.
We now present an alternative. We don’t know its original inventor(s) but do know that no one has promoted it more vigorously or explored it more extensively than S-C Chou, X-S Gao, & J-Z Zhang in their book Machine Proofs in Geometry [0].
We tentatively call it “line angle” because it associates an angle not with two rays but with two full lines, each of them extending in both directions to infinity. (This is perhaps why Chou, Gao, & Zhang speak of “full angles”.) We denote it —equally tentatively— by the infix “⌿”. It is not a symmetric function of its arguments: in fig. 7,
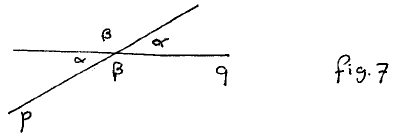
p⌿q = α and q⌿p = β . In words: p⌿q is the angle over which p must be rotated clockwise so as to make it parallel to q. The picture in fig. 7 strongly suggests p⌿q + q⌿p = π, but that is an equality we shall return to later.
What we have gained can be seen by observing how the notion of the line angle does away with the anomaly signalled in fig. 5. Consider two given points P and Q, and line p through P and line q through Q such that for some given α, p⌿q = α; the locus of the intersection point of p and q is a circle through P and Q:
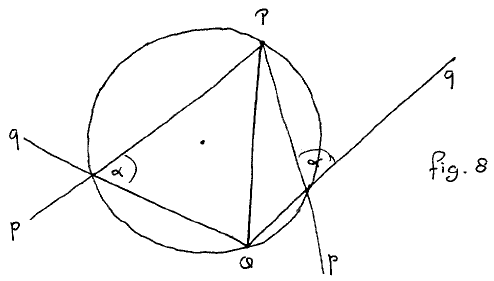
In short, the problem is solved by distinguishing the endpoints of the line segment —e.g. by naming them differently— and subsequently distinguishing the lines of a pair by the endpoint through which they pass. The convincing elegance reflected in fig. 8 is strong evidence in favour of the notion of the line angle.
We now turn our attention to fig. 3 and fig. 4, and observe that in fig. 3, in which the arcs had to be added, the arcs from A to B and from A´ to B´ are both in the clockwise direction, whereas in fig.4, where we had to take the difference of the arc lengths, one of the two —viz. from A´ to B´— goes counter-clockwise. This observation invites the introduction of the notion of the directed arc, tentatively denoted by
|
|
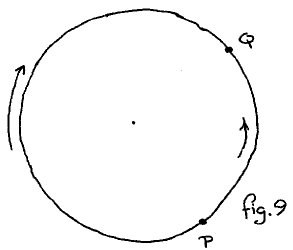
We still have to decide in which direction we count the arc length as positive. We decide that when the arc from P to Q goes in the clockwise direction, the value of
|
Clocks being what they are, arcs
|
|
|
Let line a intersect a circle in point A and A´; let line b intersect that same circle in points B and B´. Then
(0) a⌿b = (
|
|
In the above there is one issue I skimmed over. Its first manifestation is with the definition of the directed arc. The notion
|
|
Its second manifestation is with the formulation of the theorem: if line a intersects a circle, there are two points of intersection, which is A and which A´? The answer is again “either”: the difference it makes in the sum
|
is, again, an integer multiple of 2π, i.e. ignorable. (Observe the following calculation, be it written down with some notational licence:
|
=
|
|
=
|
|
Its third manifestation is with the definition of the line angle: in fig. 7 we defined p⌿q to be equal to α, the clockwise rotation from p to q. But the alternative would have been a counter-clockwise rotation over β, or, equivalently, a clockwise rotation over – β. We observe π–β = α, in general: real values that differ by an integer multiple of π represent the same line angle. With directed arcs being defined up to multiples of 2π, formula (0) now makes perfect sense, thanks to the division by 2.
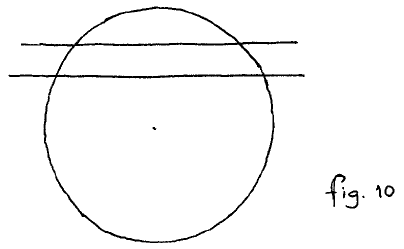
Finally, a single argument to prove lemmata 1, 2 and 3. Let us move, as in fig. 10, a line parallel to itself; the observation is that, for reasons of symmetry —and here you may be as explicit as you like— the one point of intersection moves in the counter-clockwise direction exactly as far as the other point of intersection does in the clockwise direction. Hence, if we move the line pair (a,b) parallel to itself, not only a⌿b is constant, but also
|
* * *
Having seen the alternative, the reader should realize how clumsy a theory I learned when I was young: when using Lemma 2 and/or Lemma 3, one either has to show that the intersection point lies inside/outside the circle, or one has to make a case analysis.
The point I wanted to make is that in designing a mathematical theory, the choice of concepts and definitions is crucial. I thought this was a very nice and simple example with which to drive the message home. Somehow, this note got longer than I had expected.
| [0] | Machine Proofs in Geometry, Shang-Ching Chou, Xiao-Shan Gao, Jing-Zhong Zhang, World Scientific Publishing Co, Singapore, 1994 |
Austin, 24 December 1994