Courtesy Dr.Birgit Schieder
This note deals with the proof of the following
Theorem Given are N blue and N red points in the Euclidean plane such that no 3 of them are collinear; then blue and red points can be connected one-to-one by straight line segments such that no segments intersect.
The proof is by showing the termination of the following repetition, operating on an arbitrarily initialized variable of type “one-to-one correspondence between the given N blue and N red points”:
| do | there are intersecting segments → |
| flip two intersecting segments od , |
where the operation “flip” replaces as illustrated below two intersecting segments (the solid ones) by two non-intersecting segments (the dotted ones):
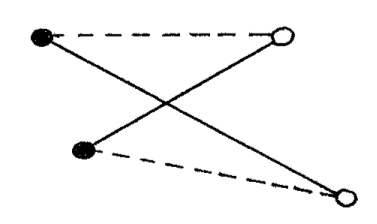
We can not conduct the proof of termination by stating that the flip reduces the number of segment/segment intersections, for it need not do so: the “dotted” segments may introduce new intersections with other segments.
The famous termination argument observes (i) that the number of possible states is finite (viz. N!), so that a real variant function will do, and (ii) that the flip decreases the sum of the lengths of the N connecting segments (and it is here that the noncollinearity is used to rule out all sorts of “pathological” cases). This argument is famous because it is also a little bit scandalous because of its illicit affaire with the notion of Euclidean distance. (It is most definitely not a metric theorem we are dealing with.) So, when I showed th above argument in 1994 at the Marktoberdorf Summer School, I challenged the audience to design a “decent” proof (i.e. using only concepts of affine geometry.) The challenge was most elegantly met by Dr.Birgit Schieder (of the “Institut für Informatik der Technischen Universität München”), who constructed a counting argument. The challenge is, firstly, to choose what to count and, secondly, to design a crisp argument for the decrease.
The changing state of the computation is characterized by the one-to-one correspondence, i.e. by the set of N connecting segments. Below, we shall use the term “segment” to denote the so-called “open” segment, i.e. its two coloured endpoints are not included. We shall use the term “line” to denote any of the N 2 infinite lines through 1 blue and 1 red point; this set of N 2 lines is as fixed as the 2N coloured points. Finally, a line and a segment are said to be “intersect”, or to give rise to an “intersection”, when they have exactly 1 point in common.
Lemma 0 For no line the number of segments it intersects is increased by a flip.
Proof
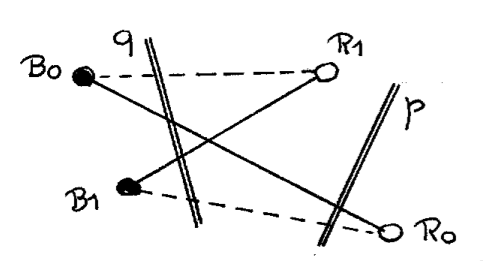
For a line whose number of intersections is possibly increased by the flip, we can confine our attention to lines that intersect at least 1 of the segments created by the flip. Representative instances are line p (intersects 1 dotted segment) and line q (intersects 2 dotted segments). But —not thanks to Euclid, but thanks to Hilbert— they intersect as many solid segments, so the flip does not increase their number of intersections. (End of Proof.)
Lemma 1 For two lines, the number of segments intersected is decreased by 1.
Proof Line (B0, R0) loses its intersection with segment (B1, R1), which disappears, and intersects neither of the new segments. Similarly for line (B1, R1) (End of Proof.)
From the lemmata we conclude that each flip decreases the number of line/segment intersections, and this concludes Birgit Schieder’s counting argument.
* *
*
I posed the problem to the Tuesday Afternoon Clubs in Eindhoven and Austin; both solved the problem. At the ETAC, we then investigated how the case analysis could be reduced, and how the argument that it is exhaustive could be simplified. (The argument as given above, however, was designed later.) At the ATAC, we afterwards looked for heuristics that would have led to the idea of counting segment/line intersections. In retrospect we could make all sorts of explanatory and justifying remarks, but none of them could in honesty be dressed up as heuristic principle.
The counting argument annoys me because my “proof” of Lemma 0 relies so heavily on that part of geometry with whose axiomatization I am so unfamiliar: I know Euclid’s axioms, but for a proof of Lemma 0 they don’t suffice.
Austin, 17 September 1995
prof.dr. Edsger W.Dijkstra
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712-1188
USA