Ulrich Berger’s argument rephrased
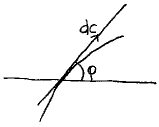
We introduce a special type of line integral, the “contour integral”, in which the differential dc is an infinitesimal vector along the tangent. [With s the length along the contour, we have
dc = (cos.φ ds, sin.φ ds).]
We only consider clockwise integrals along closed contours; hence the law ∮dc = (0,0).
We now consider for a vector field f and some contour the contour integral ∮f.(x,y)•dc, where • denotes the scalar product. We don’t need to consider “bagels” with a hole in them
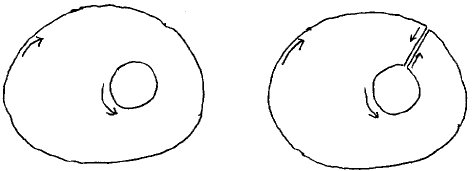
for the above two figures have equal contour integrals because the two contributions along the cut cancel.
Similarly, when we consider —like a jigsaw puzzle— a figure partitioned into a finite number of pieces, then the contour integral of the whole equals the sum of the contour integrals of the pieces. (We refer to this as “the Law”.)

Note For f.(x,y) = (y,0) or f.(x,y) = (0,–x), the contour integral equals the area enclosed by the contour, and indeed: the area of the whole jigsaw puzzle equals the sum of the areas of the pieces. (End of Note.)
* * *
We only consider rectangles with horizontal and vertical sides. A rectangle is called nice when in at least one direction it has sides of integer length. The theorem to be proved is that in the case of a large rectangle R partitioned in a finite number of little rectangles r, rectangle R is nice if all rectangles r are nice.
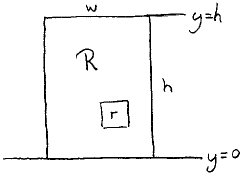
We demonstrate that, with all rectangles r nice, R has an integer width w when its height h is noninteger. We do this by introducing an f such that
| (i) | the contour integral of R equals w |
| (ii) | the contour integral of each r is integer. |
The Law then allows us to conclude that w, a sum of integers, is integer.
When we place R with its bottom at y=0 (and, hence, its top at y=h), some reflection shows that this is, for instance, realized by
f.(x,y) = (if y is integer → 0 ▯ y is not integer → 1 fi, 0)
ad (i). Only the top side, of length w, contributes to the contour integral of R, 0 being integer and h not.
ad (ii). For a rectangle whose vertical sides are of integer length, the contributions along its horizontal sides (zero or not) cancel, and for a rectangle r whose horizontal sides are of integer length, the contributions along its horizontal sides (zero or not) are integer; in either case, nice rectangle r has a contour integral of integer value.
Nuenen, 8 September 1999
prof.dr. Edsger W.Dijkstra
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712–1188
USA