Triggered by a high-school exercise
In this note, “fractions” are restricted to quotients of positive integers. If a/b and c/d are two such fractions of different values, one is asked to construct a third fraction that lies between them.
The book in which we met this problem —a textbook of Anuj Misra’s— started by giving the fractions equal denominators, so 2/3 and 3/4 would become 8/12 and 9/12, but then the problem is that there is no integer between 8 and 9; this is overcome by introducing an extra factor of 2, so that the fractions become 16/24 and 18/24 and the answer 17/24. When, later, I started to discuss this problem with an American colleague, he came up with the same solution, which made me wonder whether I had met a cultural difference between two continents because, spontaneously and indepedently, Ria and I had reacted with “What about (a+c)/(b+d)?” The reasons for writing this little note, however, are my experiences in proving the correctness of the this hunch.
I first came up with a visual proof, and later with a calculational one. In both proofs we restrict ourselves to
(0) a /b < c /d
The visual proof
Connect the points (b, a) and (d, c) to the origin and complete the parallelogram
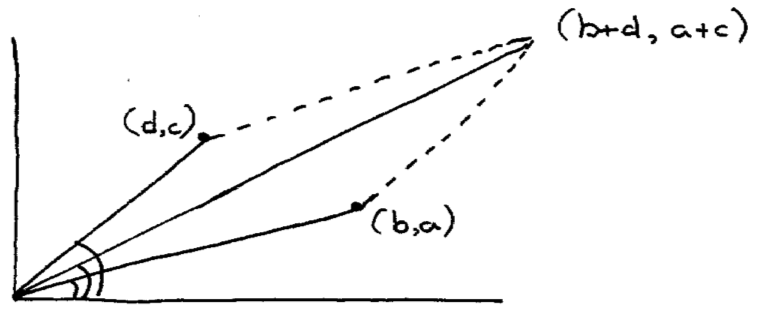
Because of the monotonicity of the tangent in the 1st quadrant and the fact the diagonal of a parallelogram lies inside that parallelogram, i.e., between the two sides, we conclude
(1) a /b < (a+c)/(b+d) < c/d
The calculational proof
For the left inequality of (1) we observe
a /b < (a+c )/(b+d )
≡ { b · (b+d ) > 0 }
a · (b+d ) < (a+c ) · b
≡ { algebra }
a · d < c · b
≡ { b · d > 0 }
a /b < c /d
A similar proof shows that also the right inequality of (1) is equivalent to (0), to which we could restrict ourselves “without loss of generality”.
* *
*
It was a few days after the problem had been shown to us when I realized that I had not taken the trouble to prove the correctness of our hunch; after a while, the visual proof came to the mind, and I must confess that it convinced me.
It was another few days later when my mind returned to the visual “proof” and I realized how shaky it was and how much it had left unsaid. It draws “conclusions” from the loosely stated fact that the diagonals lie “inside” the parallelogram, but how to prove that? In all probability by proving (1)! By not being explicit about the rules of the game and appealing to “the visual intuition” instead, one introduces a lot of ambiguity about the whole enterprise of proving. No wonder that the kids at school get confused!
After all the above I began to wonder what went into the construction of the hunch: certainly neither of the two arguments shown above. I was at least familiar with the following ingredients:
(i) fractions are monotonic functions of their numerators and antimonotonic functions of their denominators,
(ii) the whole problem is in a sense insensitive to a systematic replacement of a /b by b/a, etc.,
(iii) the problem is symmetric in the two given fractions —the word “between” makes it that—,
(iv) the sum is the first symmetric, monotonic function of integers that comes to my mind.
That probably suffices.
Austin, 16 March 2000
prof.dr. Edsger W.Dijkstra
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712–1188
USA