The river, the isles and the bridges
In a river lie 6 isles, connected by 13 bridges to each other and the shores as follows:
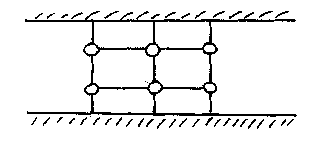
When in a storm each bridge has a probability 1/2 of being swept away. What is the probability that the shores remain connected?
* * *
We propose to associate the 13 bridges with the 13 squares in the following array
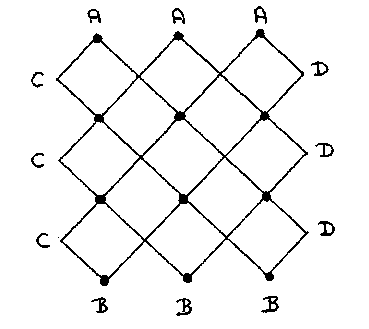
such that the original bridges correspond to the diagonals between the marked corners of the squares.
In each square we connect with probability 1/2 either
| (i) | the marked corners by a solid diagonal: | 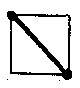 |
|
or
|
||
| (ii) | the unmarked corners by a dotted diagonal |  |
In the new terminology, we are now asking for the probability that there exists a solid path between the As and the Bs.
Paths being continuous we conclude
(As and Bs are connected by a solid path)
≢ (Cs and Ds are connected by a dotted path)
and hence
(0) the probability that As and Bs are connected
= the probability that Cs and Ds are not connected.
From the symmetry of fig. 0 and the equal probabilities of (i) and (ii) we conclude
(1) the probability that Cs and Ds are not connected
= the probability that As and Bs are not connected.
Combining (0) and (1) we conclude that the As and Bs are as likely to be connected as to be disconnected. The answer we were looking for is therefore ½ .
Remark The answer is not surprising since ½ is also the answer in the situations
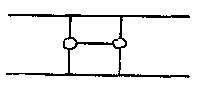
and
(End of Remark)
* *
*
I learned this problem early June from Dr. Georg Zimmermann at a workshop "Sprache und Mathematik" that the Fachschaft Mathematik of the Bischöfliche Studienförderung "Cusanuswerk" had organized in Uder. We solved the problem at the next session of the ETAC ( = Eindhoven Tuesday Afternoon Club); in particular the contribution of Frans van der Sommen is acknowledged.
And then it took me almost a month to find the time and muster the energy to record the solution. Besides the usual excuses of having other things to do, there was the fact that I still had to invent fig. 0, an invention that helped me —I think!— in my exposition, but also annoyed me because I needed pencil and paper for it.
Eventually I concluded that I did not like the problem too much: its solution remained an isolated ingenuity.
Nuenen, 10 July 2000
prof.dr Edsger W.Dijkstra
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712-1188
USA