[Editorial note: To obtain the full images when you print this document, you should choose landscape orientation rather than portrait orientation]
Bruce A. Wooley
Department of Computer Science
Mississippi State University
Mississippi State, MS 39762
(601) 325-8073
bwooley.cs.msstate.edu
ABSTRACT
The data-mining step in knowledge discovery is computationally expensive when working with large data-sets. Clustering is one form of unsupervised learning used in data mining. I am adapting a Meta learning approach, used to scale supervised learning, to scale unsupervised learning. This approach allows a variety of clustering algorithms to be used for the base classification systems and then learns relationships among the base classification systems to accomplish final predictions. The base classifiers may be executed on independent computers accomplishing processor scaling as well as data scaling.
INTRODUCTION
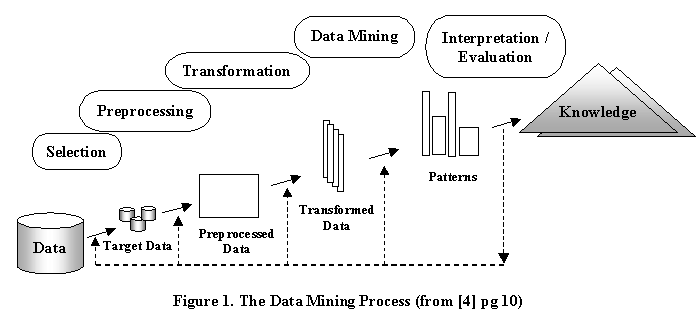
Knowledge discovery in databases (KDD) is a process consisting of multiple steps that may be performed iteratively to glean bits of knowledge from large databases [4]. An example of the KDD is shown in Figure 1. The data-mining step of the KDD process usually uses concepts from machine learning to accomplish classification, clustering or model fitting to the data. Most of the learning algorithms used in data-mining are either supervised learning or unsupervised learning. Supervised learning requires a training set of sample elements along with the desired classification of each of these samples. Unsupervised learning also requires a training set of sample elements, however there is no knowledge about the classification of these training samples. Unsupervised learning has both advantages and disadvantages over supervised learning. The major disadvantage is the lack of direction for the learning algorithm and that there may not be any interesting knowledge discovered in the set of features selected for the training. This lack of direction also turns out to be an advantage, because it lets the algorithm look for patterns that have not previously been considered.
Clustering is a form of unsupervised learning that finds patterns in the data by putting each data element into one of K clusters, where each cluster contains data elements most similar to each other. There is a variety of clustering algorithms that use feature vectors to determine the clusters. These algorithms may use neural networks, statistics, or probabilities to perform clustering, and they iterate over the data to compute the categories that describe the data. Most of these clustering algorithms require all the data to be kept in RAM while they iterate through the data computing new statistics for each cluster to improve the mapping of the elements to the clusters based on the features for each element. There are two problems inherent to using most clustering algorithms to process very large databases. The first problem is determining how to process the data without having it all in RAM at one time, and the second problem is how to complete all the computation in a reasonable amount of time. [1] and [6] address the first problem of scaling the data by creating a large number of cluster descriptors called cluster features (CFs) that maintain statistics of a larger set of data elements. The cluster features are then used as input to a statistical clustering algorithm.
Most of the research in scaling data mining is in supervised learning or in modification of algorithms to create statistical information about subsets of the data [1] and [9]. My research addresses both of the problems listed above, the scaling of the data and the decrease in processing time through parallelization.
DESCRIPTION OF RESEARCH
My dissertation research is to develop a scalable clustering system by using a Meta learning technique to train a classifier system built from multiple independent base classifiers. Each of the base classifiers is trained independently which allows the scaling of both data and processing as well as a choice of classifier algorithms for each of the base classifiers. I am adapting an approach used by [3] (scaling supervised learning) to work with clustering algorithms. This approach divides the data into P disjoint data-sets and trains P independent base classifiers. Each of the P base-classifiers is trained to place elements into one of K categories. The K categories from each of the P base classifiers need to be cross referenced to identify which category from a specific base classifier corresponds to a specific category from another base classifier. This problem of correlating the results from independent classifiers does not exist in supervised learning since the correct answer is known for each of the elements in the training data. I accomplish this correlation by processing all the training data through each of the base classifiers and cross-referencing their results.
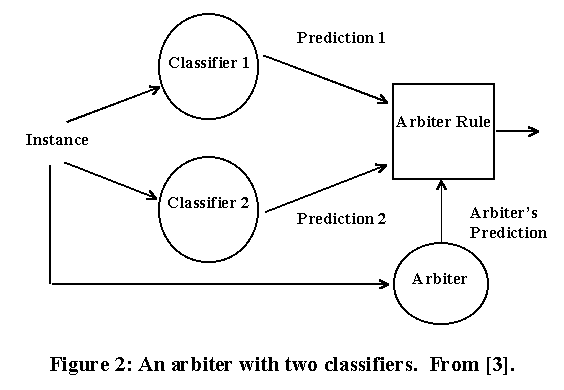
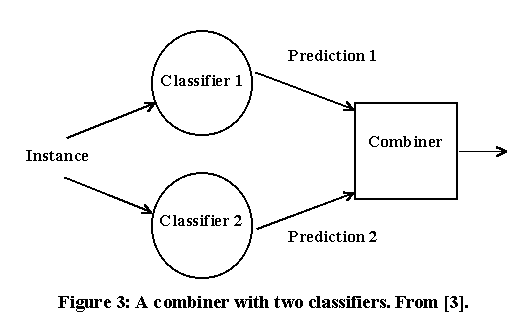
I am using two specific strategies adapted from Chan and Stolfo's [3] Meta learning techniques. The first strategy uses an arbitration rule and an arbiter [9] pictured in Figure 2, and the second strategy uses a combiner as pictured in Figure 3.

The first step of the training phase divides all the training instances (I1 .. Ix) into P disjoint data sets (D1 .. DP), which are then distributed to the P processors and used to train the P independent classifiers (C1 .. CP). Each classifier identifies a number of classes from its training data. The jth class of classifier Ci is notated cij. The second step of the training phase is dependent on the type of Meta training you choose.
The second step of the training phase for the arbiter is for each of the classifiers (C1 .. CP) to predict the appropriate classes for all of the original training instances (I1 .. Ix). From this I create a P dimensional matrix M using the classes of each of the Ci for each instance as indices to the matrix (M[c1j', c2j'', cPj'']) and increment the matrix element identified. Finally, each of the matrix elements that exceed some threshold value (a function of the instances (I1 .. Ix) and the number of independent classifiers P) is considered a class in the final system. Predictions on new instances is accomplished by obtaining the prediction from each of the Ci classifiers and finding the class identified by the associated matrix element M[c1j', c2j'', cPj'''']. If this matrix element did not meet the threshold requirements, then use the arbiter to identify the class. For my experiments, the arbiter just placed these instances into one class that was different from any identified by the matrix.
The second step of the training phase for the combiner chooses a subset of the original training instances that include instances used in training each of the Ci classifiers. The P classifiers predict the class for each of the instances, and the P classes for each instance is combined into a new training vector for that instance. An unsupervised learning system is then used to learn associations between the P classifiers. Predictions on new instances is accomplished by obtaining the prediction form each of the Ci classifiers, building a new feature vector for this instance from the classes identified by the base classifiers, and predicting the class of this new feature vector from the final classifier.
RESULTS
I applied this technique to the process of provincing the ocean floor from sonar images [2], [5], [7], [8], [9]. The speedup for 2 to 5 processors is linear and I hope to increase the bandwidth so this linear speed up will continue beyond 30 processors. The images resulting from applying multiple classifiers are comparable to the images resulting by training a single classification system. The most notable difference is that the regions associated with noise tend to have less influence and are absorbed into categories defined by other regions.
ACKNOWLEDGEMENTS
I would like to thank Dr. Susan Bridges and Dr, Julia Hodges for all their support in my research. This research is supported by the Office of Naval Research under grant ONR-N00014-96-1276, by the Mississippi State University College of Engineering under the Hearin Educational Enhancement Fund, and by NASA Stennis under grant NAS1398033-20-99010033.
REFERENCES
[1] Bradley, P. S., Usama Fayyad, and Cory Reina. 1998. Scaling clustering algorithms to large databases. In Proceedings of the Fourth International Conference on Knowledge Discovery and Data Mining. Edited by Rakesh Agrawal and Paul Stolorz. Menlo Park, CA: AAAI Press. 9-15.
[2] Bridges, Susan, Julia Hodges, Bruce Wooley, Donald Karpovich, George Brannon Smith. 1998. Knowledge discovery in an oceanographic database. Submitted for publication.
[3] Chan, Philip K., and Salvatore J. Stolfo. 1995. Learning arbiter and combiner trees from partitioned data for scaling machine learning. In Proceedings of the First International Conference on Knowledge Discovery and Data Mining. Edited by Usama Fayyad and Ramasamy Uthurusamy. Menlo Park, CA: AAAI Press. 39-44.
[4] Fayyad, Usama M., Gregory Piatetsky-Shapiro, and Padhraic Smyth. 1996. From data mining to knowledge discovery: An overview. Advances in knowledge discovery and data mining. Edited by Usama M. Fayyad, Gregory Piatetsky-Shapiro, Padhraic Smyth, and Ramasamy Uthurusamy. Menlo Park, CA: AAAI Press. 1-36.
[5] Karpovich, Donald. 1998. Choosing the optimal features and texel sizes in image categorization. In Proceedings of the 36th ACM Southeast Conference held in Marietta, GA, April 1-3, 1998. 104-107
[6] Livny, Miron, Raghu Ramakrishnan, and Tian Zhang. 1998. Fast density and probability estimation using CF-Kernel method for very large databases. http://www.cs.wisc.edu/~zhang/birch.html, accessed Oct 1998.
[7] Reed, Thomas Beckett IV, and Donald Hussong. 1989. Digital image processing techniques for enhancement and classification of SeaMARC II side scan sonar imagery. Journal of Geophysical Research. 94(B6). 7469-7490.
[8] Wooley, Bruce and George Brannon Smith. 1998. Region-growing techniques based on texture for provincing the ocean floor. In Proceedings of the 36th ACM Southeast Conference held in Marietta, GA, April 1-3, 1998. 99-103.
[9] Wooley, Bruce, Yoginder Dandass, Susan Bridges, Julia Hodges, And Anthony Skjellum. 1998. Scalable knowledge discovery from oceanographic data. In Intelligent engineering systems through artificial neural networks. Volume 8 (ANNIE 98). Edited by Cihan H Dagli, Metin Akay, Anna L Buczak, Okan Ersoy, and Benito R. Fernandez. New York, NY: ASME Press. 413-24.