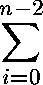Complexity Analysis

An essential aspect to data structures is algorithms. Data structures are implemented using algorithms. An algorithm is a procedure that you can write as a C function or program, or any other language. An algorithm states explicitly how the data will be manipulated.

Algorithm Efficiency

Some algorithms are more efficient than others. We would prefer to chose an efficient algorithm, so it would be nice to have metrics for comparing algorithm efficiency.

The complexity of an algorithm is a function describing the efficiency of the algorithm in terms of the amount of data the algorithm must process. Usually there are natural units for the domain and range of this function. There are two main complexity measures of the efficiency of an algorithm:

Time complexity is a function describing the amount of time an algorithm takes in terms of the amount of input to the algorithm. "Time" can mean the number of memory accesses performed, the number of comparisons between integers, the number of times some inner loop is executed, or some other natural unit related to the amount of real time the algorithm will take. We try to keep this idea of time separate from "wall clock" time, since many factors unrelated to the algorithm itself can affect the real time (like the language used, type of computing hardware, proficiency of the programmer, optimization in the compiler, etc.). It turns out that, if we chose the units wisely, all of the other stuff doesn't matter and we can get an independent measure of the efficiency of the algorithm.
Space complexity is a function describing the amount of memory (space) an algorithm takes in terms of the amount of input to the algorithm. We often speak of "extra" memory needed, not counting the memory needed to store the input itself. Again, we use natural (but fixed-length) units to measure this. We can use bytes, but it's easier to use, say, number of integers used, number of fixed-sized structures, etc. In the end, the function we come up with will be independent of the actual number of bytes needed to represent the unit. Space complexity is sometimes ignored because the space used is minimal and/or obvious, but sometimes it becomes as important an issue as time.

For example, we might say "this algorithm takes n² time," where n is the number of items in the input. Or we might say "this algorithm takes constant extra space," because the amount of extra memory needed doesn't vary with the number of items processed.

For both time and space, we are interested in the asymptotic complexity of the algorithm: When n (the number of items of input) goes to infinity, what happens to the performance of the algorithm?

An example: Selection Sort

Suppose we want to put an array of n floating point numbers into ascending numerical order. This task is called sorting and should be somewhat familiar. One simple algorithm for sorting is selection sort. You let an index i go from 0 to n-1, exchanging the ith element of the array with the minimum element from i up to n. Here are the iterations of selection sort carried out on the sequence {4 3 9 6 1 7 0}:

index	0	1	2	3	4	5	6	comments
---------------------------------------------------------	--------
    |	4	3	9	6	1	7	0	initial
i=0 |	0	3	9	6	1	7	4	swap 0,4
i=1 |	0	1	9	6	3	7	4	swap 1,3
i=2 |	0	1	3	6	9	7	4	swap 3, 9
i=3 |	0	1	3	4	9	7	6	swap 6, 4
i=4 |	0	1	3	4	6	7	9	swap 9, 6
i=5 |	0	1	3	4	6	7	9	(done)

Here is a simple implementation in C:

int find_min_index (float [], int, int);
void swap (float [], int, int);

/* selection sort on array v of n floats */

void selection_sort (float v[], int n) {
	int	i;

	/* for i from 0 to n-1, swap v[i] with the minimum
	 * of the i'th to the n'th array elements
	 */
	for (i=0; i<n-1; i++) 
		swap (v, i, find_min_index (v, i, n));
}

/* find the index of the minimum element of float array v from
 * indices start to end
 */
int find_min_index (float v[], int start, int end) {
	int	i, mini;

	mini = start;
	for (i=start+1; i<end; i++) 
		if (v[i] < v[mini]) mini = i;
	return mini;
}

/* swap i'th with j'th elements of float array v */
void swap (float v[], int i, int j) {
	float	t;

	t = v[i];
	v[i] = v[j];
	v[j] = t;
}

Now we want to quantify the performance of the algorithm, i.e., the amount of time and space taken in terms of n. We are mainly interested in how the time and space requirements change as n grows large; sorting 10 items is trivial for almost any reasonable algorithm you can think of, but what about 1,000, 10,000, 1,000,000 or more items?

For this example, the amount of space needed is clearly dominated by the memory consumed by the array, so we don't have to worry about it; if we can store the array, we can sort it. That is, it takes constant extra space.

So we are mainly interested in the amount of time the algorithm takes. One approach is to count the number of array accesses made during the execution of the algorithm; since each array access takes a certain (small) amount of time related to the hardware, this count is proportional to the time the algorithm takes.

We will end up with a function in terms of n that gives us the number of array accesses for the algorithm. We'll call this function T(n), for Time.

T(n) is the total number of accesses made from the beginning of selection_sort until the end. selection_sort itself simply calls swap and find_min_index as i goes from 0 to n-1, so

T(n) = [ time for swap + time for find_min_index (v, i, n)] .

(n-2 because the for loop goes from 0 up to but not including n-1). (Note: for those not familiar with Sigma notation, that nasty looking formula above just means "the sum, as we let i go from 0 to n-2, of the time for swap plus the time for find_min_index (v, i, n).) The swap function makes four accesses to the array, so the function is now

T(n) = [ 4 + time for find_min_index (v, i, n)] .

If we look at find_min_index, we see it does two array accesses for each iteration through the for loop, and it does the for loop n - i - 1 times:

T(n) = [ 4 + 2 (n - i - 1)] .

With some mathematical manipulation, we can break this up into:

T(n) = 4(n-1) + 2n(n-1) - 2(n-1) - 2 i .

(everything times n-1 because we go from 0 to n-2, i.e., n-1 times). Remembering that the sum of i as i goes from 0 to n is (n(n+1))/2, then substituting in n-2 and cancelling out the 2's:

T(n) = 4(n-1) + 2n(n-1) - 2(n-1) - ((n-2)(n-1)).

and to make a long story short,

T(n) = n² + 3n - 4 .

So this function gives us the number of array accesses selection_sort makes for a given array size, and thus an idea of the amount of time it takes. There are other factors affecting the performance, for instance the loop overhead, other processes running on the system, and the fact that access time to memory is not really a constant. But this kind of analysis gives you a good idea of the amount of time you'll spend waiting, and allows you to compare this algorithms to other algorithms that have been analyzed in a similar way.

Another algorithm used for sorting is called merge sort. The details are somewhat more complicated and will be covered later in the course, but for now it's sufficient to state that a certain C implementation takes T_m(n) = 8n log n memory accesses to sort n elements. Let's look at a table of T(n) vs. T_m(n):

 n	T(n)	T_m(n)
---	----	-----
2	6	11
3	14	26
4	24	44
5	36	64
6	50	86
7	66	108
8	84	133
9	104	158
10	126	184
11	150	211
12	176	238
13	204	266
14	234	295
15	266	324
16	300	354
17	336	385
18	374	416
19	414	447
20	456	479

T(n) seems to outperform T_m(n) here, so at first glance one might think selection sort is better than merge sort. But if we extend the table:

 n	T(n)	T_m(n)
---	----	-----
20	456	479
21	500	511
22	546	544
23	594	576
24	644	610
25	696	643
26	750	677
27	806	711
28	864	746
29	924	781
30	986	816

we see that merge sort starts to take a little less time than selection sort for larger values of n. If we extend the table to large values:

 n		T(n)			T_m(n)
---		----			-----
100     	10,296    		3,684
1,000    	1,002,996  		55,262
10,000   	100,029,996       	736,827
100,000  	10,000,299,996     	9,210,340
1,000,000 	1,000,002,999,996   	110,524,084
10,000,000      100,000,029,999,996 	1,289,447,652

we see that merge sort does much better than selection sort. To put this in perspective, recall that a typical memory access is done on the order of nanoseconds, or billionths of a second. Selection sort on ten million items takes roughly 100 trillion accesses; if each one takes ten nanoseconds (an optimistic assumption based on 1998 hardware) it will take 1,000,000 seconds, or about 11 and a half days to complete. Merge sort, with a "mere" 1.2 billion accesses, will be done in 12 seconds. For a billion elements, selection sort takes almost 32,000 years, while merge sort takes about 37 minutes. And, assuming a large enough RAM size, a trillion elements will take selection sort 300 million years, while merge sort will take 32 days. Since computer hardware is not resilient to the large asteroids that hit our planet roughly once every 100 million years causing mass extinctions, selection sort is not feasible for this task. (Note: you will notice as you study CS that computer scientists like to put things in astronomical and geological terms when trying to show an approach is the wrong one. Just humor them.)

Asymptotic Notation

This function we came up with, T(n) = n² + 3n - 4, describes precisely the number of array accesses made in the algorithm. In a sense, it is a little too precise; all we really need to say is n²; the lower order terms contribute almost nothing to the sum when n is large. We would like a way to justify ignoring those lower order terms and to make comparisons between algorithms easy. So we use asymptotic notation.

Big O

The most common notation used is "big O" notation. In the above example, we would say n² + 3n - 4 = O(n²) (read "big oh of n squared"). This means, intuitively, that the important part of n² + 3n - 4 is the n² part.

Definition: Let f(n) and g(n) be functions, where n is a positive integer. We write f(n) = O(g(n)) if and only if there exists a real number c and positive integer n₀ satisfying 0 <= f(n) <= cg(n) for all n >= n₀. (And we say, "f of n is big oh of g of n." We might also say or write f(n) is in O(g(n)), because we can think of O as a set of functions all with the same property. But we won't often do that in Data Structures.)

This means that, for example, that functions like n² + n, 4n² - n log n + 12, n²/5 - 100n, n log n, 50n, and so forth are all O(n²). Every function f(n) bounded above by some constant multiple g(n) for all values of n greater than a certain value is O(g(n)).

Examples:

Show 3n² + 4n - 2 = O(n²).
We need to find c and n₀ such that:
3n² + 4n - 2 <= cn² for all n >= n₀ .
Divide both sides by n², getting:
3 + 4/n - 2/n² <= c for all n >= n₀ .
If we choose n₀ equal to 1, then we need a value of c such that:
3 + 4 - 2 <= c
We can set c equal to 6. Now we have:
3n² + 4n - 2 <= 6n² for all n >= 1 .
Show n³ != O(n^{2).
Let's assume to the contrary that

n³ = O(n²)

Then there must exist constants c and n₀ such that

n³ <= cn² for all n >=
n₀.

Dividing by n^{2, we get:

n <= c for all n >=
n₀.

But this is not possible; we can never choose a constant c
large enough that n will never exceed it, since n
can grow without bound. Thus, the original assumption, that
n³ = O(n²), must
be wrong so n³ != O(n²).}}

Big O gives us a formal way of expressing asymptotic upper bounds, a way of bounding from above the growth of a function. Knowing where a function falls within the big-O hierarchy allows us to compare it quickly with other functions and gives us an idea of which algorithm has the best time performance. And yes, there is also a "little o" we'll see later.

Properties of Big O

The definition of big O is pretty ugly to have to work with all the time, kind of like the "limit" definition of a derivative in Calculus. Here are some helpful theorems you can use to simplify big O calculations:

Any k^th degree polynomial is O(n^k).
a n^k = O(n^k) for any a > 0.
Big O is transitive. That is, if f(n) = O(g(n)) and g(n) is O(h(n)), then f(n) = O(h(n)).
log_an = O(log_b n) for any a, b > 1. This practically means that we don't care, asymptotically, what base we take our logarithms to. (I said asymptotically. In a few cases, it does matter.)
Big O of a sum of functions is big O of the largest function. How do you know which one is the largest? The one that all the others are big O of. One consequence of this is, if f(n) = O(h(n)) and g(n) is O(h(n)), then f(n) + g(n) = O(h(n)).
f(n) = O(g(n)) is true if lim_n->infinityf(n)/g(n) is a constant.

Lower Bounds and Tight Bounds

Big O only gives you an upper bound on a function, i.e., if we ignore constant factors and let n get big enough, we know some function will never exceed some other function. But this can give us too much freedom. For instance, the time for selection sort is easily O(n³), because n² is O(n³). But we know that O(n²) is a more meaningful upper bound. What we need is to be able to describe a lower bound, a function that always grows more slowly than f(n), and a tight bound, a function that grows at about the same rate as f(n). Your book give a good theoretical introduction to these two concepts; let's look at a different (and probably easier to understand) way to approach this.

Big Omega is for lower bounds what big O is for upper bounds:

Definition: Let f(n) and g(n) be functions, where n is a positive integer. We write f(n) = (g(n)) if and only if g(n) = O(f(n)). We say "f of n is omega of g of n."

This means g is a lower bound for f; after a certain value of n, and without regard to multiplicative constants, f will never go below g.

Finally, theta notation combines upper bounds with lower bounds to get tight bounds:

Definition: Let f(n) and g(n) be functions, where n is a positive integer. We write f(n) = (g(n)) if and only if g(n) = O(f(n)). and g(n) = (f(n)). We say "f of n is theta of g of n."

More Properties

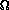The first four properties listed above for big O are also true for Omega and Theta.
Replace O with and "largest" with "smallest" in the fifth property for big O and it remains true.
f(n) = (g(n)) is true if lim_n->infinityg(n)/f(n) is a constant.
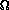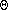f(n) = (g(n)) is true if lim_n->infinityf(n)/g(n) is a non-zero constant.
n^k = O((1+) ⁿ)) for any positive k and . That is, any polynomial is bound from above by any exponential. So any algorithm that runs in polynomial time is (eventually, for large enough value of n) preferable to any algorithm that runs in exponential time.
(log n) = O(n^k) for any positive k and . That means a logarithm to any power grows more slowly than a polynomial (even things like square root, 100th root, etc.) So an algorithm that runs in logarithmic time is (eventually) preferable to an algorithm that runs in polynomial (or indeed exponential, from above) time.