Algorithms for Permutations and Combinations
Here are some algorithms I have found useful in surprisingly many
instances:
Generating Permutations of a Set of Elements
We know that there are n! permutations of n
elements; we have seen this fact when e.g. proving lower bounds on
comparison sorting and the brute-force algorithm for solving the
Travelling Salesman Problem. But how do we generate these permutations?
The following algorithm, presented as a C program that prints the
permutations of the first 5 positive integers, can be adapted to
generated permutations of any kind of element you want:
#include <stdio.h>
/* function to swap array elements */
void swap (int v[], int i, int j) {
int t;
t = v[i];
v[i] = v[j];
v[j] = t;
}
/* recursive function to generate permutations */
void perm (int v[], int n, int i) {
/* this function generates the permutations of the array
* from element i to element n-1
*/
int j;
/* if we are at the end of the array, we have one permutation
* we can use (here we print it; you could as easily hand the
* array off to some other function that uses it for something
*/
if (i == n) {
for (j=0; j<n; j++) printf ("%d ", v[j]);
printf ("\n");
} else
/* recursively explore the permutations starting
* at index i going through index n-1
*/
for (j=i; j<n; j++) {
/* try the array with i and j switched */
swap (v, i, j);
perm (v, n, i+1);
/* swap them back the way they were */
swap (v, i, j);
}
}
/* little driver function to print perms of first 5 integers */
int main () {
int v[5], i;
for (i=0; i<5; i++) v[i] = i+1;
perm (v, 5, 0);
exit (0);
}
Note that the running time of this program, in terms of the number of
times a permutation is printed, is exactly n!, so it is as efficient
as it can be since it necessarily does n! things.
What about the space complexity? Aside from the array itself, which
consumes 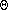 (n) storage,
we have recursion consuming stack frames. If we trace the recursion from
the top level invokation down to the base case, we easily see that
no more than O(n) invokations are done before returning
up the tree of recursive calls. Thus, only up to O(n)
stack frames are needed.
(n) storage,
we have recursion consuming stack frames. If we trace the recursion from
the top level invokation down to the base case, we easily see that
no more than O(n) invokations are done before returning
up the tree of recursive calls. Thus, only up to O(n)
stack frames are needed.
Note that this algorithm will take forever when n gets beyond
15 or so.
Generating Combinations of a Set of Elements
A related problem is that of generating combinations of a set
of n elements taken k at a time without replacement.
This problem comes up frequently in real world situations, for instance
when you need to compute a list of groups of people that could be assigned
to a group. On the Usenet newsgroups sci.math
and comp.theory , this question comes up
about once a month, and probably even more often in programming newsgroups.
Here is a very simple algorithm that will do this for you. The nice thing
about it is that the concept is easy to remember and code up; it always
seems that when you need an algorithm like this, the book you saw it in
is somewhere else or the computer you have it on is inaccessible, so being
able to code it up on the fly is a nice property.
The quantity we are interested in is n choose k,
abbreviated n C k. Let's represent the elements
of a set as an array of bits. If the bit is 1, then the element
is in the set, otherwise the element is not in the set. For example,
the following binary number:
11010101
with bit numbers running from 7 down to 0, represents the set:
{ 7 6 4 2 0 }
If we want to generated all n C k combinations of
n integers from 0..n-1 taken k at a time,
we can just generate all binary numbers with exactly k 1-bits.
The simple (but inefficient) way to do this is just generate all possible
n-bit numbers, count the bits in each, and print the corresponding
combination when the number of bits is equal to k. Here is
the algorithm, in awful bit-twiddling C (printing sets of integers beginning
with 1 instead of 0). Note that in C, 1 << n is the same
as 2n:
/* This program accepts n and k on the command line, then prints
* all n C k combinations of integers from 1..n
*/
#include <stdio.h>
int main (int argc, char *argv[]) {
int n, k, i, j, c;
if (argc != 3) {
printf ("Usage: %s n k\n", argv[0]);
exit (1);
}
n = atoi (argv[1]);
k = atoi (argv[2]);
/* i goes through all n-bit numbers */
for (i=0; i<(1<<n); i++) {
/* masking the j'th bit as j goes through all the bits,
* count the number of 1 bits. this is called finding
* a population count.
*/
for (j=0,c=0; j<32; j++) if (i & (1<<j)) c++;
/* if that number is equal to k, print the combination... */
if (c == k) {
/* by again going through all the bits indices,
* printing only the ones with 1-bits
*/
for (j=0;j<32; j++) if (i & (1<<j)) printf ("%i ", j+1);
printf ("\n");
}
}
exit (0);
}
If you don't like that code, let that be a lesson to you about avoiding
bit-twiddling in C :-). If you do like the code, get some help for that.
What is the running time of this program? Well, the trick answer
is O(1). Since C is limited to 32-bit integers, it can only
iterate up to a constant number of times. However, if we analyze the
underlying algorithm (assuming arbitrary length integers), we can see
that a population count (the first for (j... loop) takes
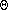 (n), and is followed by
another similar
(n), and is followed by
another similar 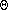 (n)
section of code, so the whole inner loop takes
(n)
section of code, so the whole inner loop takes
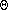 (n). The outer loop
iterates 2n times, so the whole thing takes
(n). The outer loop
iterates 2n times, so the whole thing takes
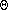 (n 2n)
times.
(n 2n)
times.
This is pretty bad for large values of n.
For example, when n = 50 and k = 2, there are
1225 combinations. However, the algorithm will iterate through
1,125,899,906,842,624 combinations before it is finished. You
shouldn't use this program for anything beyond n = 20 or so,
but it will do (just like bubble sort) in many instances. The main
adantages of this algorithm are that it is easy to implement and remember,
and gives an outlet for C hackers who like bit-twiddling.
Here is another algorithm that does the same thing more efficiently
and more incomprehensibly:
#include <stdio.h>
#include <stdlib.h>
void combinations (int v[], int start, int n, int k, int maxk) {
int i;
/* k here counts through positions in the maxk-element v.
* if k > maxk, then the v is complete and we can use it.
*/
if (k > maxk) {
/* insert code here to use combinations as you please */
for (i=1; i<=maxk; i++) printf ("%i ", v[i]);
printf ("\n");
return;
}
/* for this k'th element of the v, try all start..n
* elements in that position
*/
for (i=start; i<=n; i++) {
v[k] = i;
/* recursively generate combinations of integers
* from i+1..n
*/
combinations (v, i+1, n, k+1, maxk);
}
}
int main (int argc, char *argv[]) {
int v[100], n, k;
if (argc != 3) {
printf ("Usage: %s n k\n", argv[0]);
exit (1);
}
n = atoi (argv[1]);
k = atoi (argv[2]);
/* generate all combinations of n elements taken
* k at a time, starting with combinations containing 1
* in the first position.
*/
combinations (v, 1, n, 1, k);
exit (0);
}
How long does this algorithm take, in terms of the number recursive
calls needed to print all the combinations?
Each combination that is generated is printed (unlike before),
and it takes O(n) recursive invokations for each
combination printed, so an upper bound on the number of recursive
calls is O(n (n C k)). This algorithm
is as efficient as it can get, since you have to do about n
things to print a combination, anyway.
Permutations and Combinations
Note that you can get all permutations of n things taken
k at a time by simply calling perm (v, maxk, 0);
at the base case of combinations. This generates all
k! permutations of each of the n C k
combinations, taking O(k! n (n C k))
= O((n+1)!/(n-k)!) time.
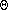 (n) storage,
we have recursion consuming stack frames. If we trace the recursion from
the top level invokation down to the base case, we easily see that
no more than O(n) invokations are done before returning
up the tree of recursive calls. Thus, only up to O(n)
stack frames are needed.
(n) storage,
we have recursion consuming stack frames. If we trace the recursion from
the top level invokation down to the base case, we easily see that
no more than O(n) invokations are done before returning
up the tree of recursive calls. Thus, only up to O(n)
stack frames are needed.