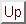of a network is the linear
transformation of it input
of a network is the linear
transformation of it input  plus some output noise
plus some output noise  ,
i.e.,
,
i.e.,  , and both input
, and both input  and
noise
and
noise 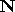 are Gaussian signals. Without losing generality,
suppose that the network capacity is 1.
are Gaussian signals. Without losing generality,
suppose that the network capacity is 1.

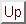

Suppose that the output  of a network is the linear
transformation of it input
of a network is the linear
transformation of it input  plus some output noise
plus some output noise  ,
i.e.,
,
i.e.,  , and both input
, and both input  and
noise
and
noise 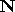 are Gaussian signals. Without losing generality,
suppose that the network capacity is 1.
are Gaussian signals. Without losing generality,
suppose that the network capacity is 1.
The optimal information transmition requires to choose the
transformation  which maximizes the information of the ouput
about the input while keeping the output variance equal to the capacity.
This can be easily solved by Lagrangian multiplier method through
maximizing
which maximizes the information of the ouput
about the input while keeping the output variance equal to the capacity.
This can be easily solved by Lagrangian multiplier method through
maximizing

in which the first term is the information of the output about the input
and the second term is the Lagangian multiplier. The derivative of  at the maximum is
at the maximum is

The solution is  and
and  ,
i.e., the output activities are decorrelated.
,
i.e., the output activities are decorrelated.
The dynamics of feedforward connections is very similar to the feedback
case. We are not going into the detail of that since our emphasis is on
the feedback path. The dynamic stability and information optimization
still hold. It is not difficult to show that the functions  and
and
 shown earlier are still the Lyapunov function and Lagrangian
function, respectively, for the joint dynamics of feedforward and
feedback connections. The decorrelation of output activities is still
the stable solution.
shown earlier are still the Lyapunov function and Lagrangian
function, respectively, for the joint dynamics of feedforward and
feedback connections. The decorrelation of output activities is still
the stable solution.