
It was pointed out in Bapi et al. [4] that it is possible to use the ACTION network to achieve attentional control. That will be explored more fully here analytically. The experiment being analysed is that of Chelazzi et al. [8] in which a monkey is trained to make an eye movement to a target (such as a square) in an array of similar shapes, of which the target had been seen a brief period earlier, but then removed while the monkey holds to the fixation point until the appearance of the array. Neuronal responses varied; for a neuron whose receptive field contained the target, the response was one of increase on appearance of the array, until the eye movement occurred. For a neuron whose receptive field did not contain the target, but another shape in the array, the neuron's activity first grew, but then decreased, as if suppressed by the first neuron whose receptive field contained the target. The relevant neuronal activities can be modelled by an ACT network which, to simplify the analysis, will be taken as composed of only two neurons. Again, to simplify, the value of n will be taken as 1. Then the equations for the two sets of neurons in the ACT net will be:
where the two sets of neurons are denoted by the unprimed and primed
variables respectively, and w is the strength of the lateral inhibition
between them (the matrix elements of  in equation (27)).
in equation (27)).
In order to analyse how this coupled system could explain the results
of Chelazzi et al. [8], a simplified version will be taken in which
the function  is replaced by its linearised form, but the
function
is replaced by its linearised form, but the
function  is kept to be non-linear. After some manipulation, and use
of the time shifting operator
is kept to be non-linear. After some manipulation, and use
of the time shifting operator  and its inverse
and its inverse
 , it is possible to obtain the coupled
set of equations for the asymptotic behaviour of x and
, it is possible to obtain the coupled
set of equations for the asymptotic behaviour of x and  as:
as:
To first order in the lateral interaction w between the two sets of unprimed and primed variables the equations (38) become
By suitable change of the constants, these may be reduced to the pair
The asymptotic values  ,
,  of the activities x,
of the activities x, 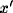 therefore
satisfy the equations
therefore
satisfy the equations
It is possible to see that these have a solution  close to 1 and
close to 1 and
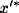 close to 0 if B>>C and
close to 0 if B>>C and  . Since
. Since 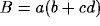 ,
,  ,
,
 and
and  , these inequalities are satisfied
provided that, for example,
, these inequalities are satisfied
provided that, for example,  . This corresponds to the learning of
the connection from the cortex to the striatum for the undashed input, and
will lead to the same qualitative behaviour in time for
. This corresponds to the learning of
the connection from the cortex to the striatum for the undashed input, and
will lead to the same qualitative behaviour in time for  and
and  as observed in the activities of the temporal lobe neurons of Chelazzi
et al. [8]. An important feature of the results of that reference is the
form of the continued activity in the delay period of the relevant neurons in
IT. If the activity is persistent then the parameters in (41) must
allow for this; if not, then the activity will ultimately die away.
Either case can be included in the above analysis, but nothing can be
concluded until the data is clarified as to this point (for example,
what length of delay can the subjects hold the memory for?).
as observed in the activities of the temporal lobe neurons of Chelazzi
et al. [8]. An important feature of the results of that reference is the
form of the continued activity in the delay period of the relevant neurons in
IT. If the activity is persistent then the parameters in (41) must
allow for this; if not, then the activity will ultimately die away.
Either case can be included in the above analysis, but nothing can be
concluded until the data is clarified as to this point (for example,
what length of delay can the subjects hold the memory for?).