
Rather than describing the distribution of each individual vector and matrix directly, the PLAPACK infrastructure requires the distribution of (imaginary) template vectors and matrices to be described. Vector and matrix distribution is given by indicating alignment with respect to these template vectors and matrices.
Imagine an infinite length vector t , which is partitioned like

with all ![]() of uniform length
of uniform length ![]() , the
distribution blocking size (see Figure 2.1).
Sub-vectors are assigned to the logical two-dimensional
mesh corresponding to the communicator (mentioned above)
by wrapping in
column-major order:
, the
distribution blocking size (see Figure 2.1).
Sub-vectors are assigned to the logical two-dimensional
mesh corresponding to the communicator (mentioned above)
by wrapping in
column-major order:
![]() is assigned to
is assigned to
![]() ,
as illustrated in Figure 2.1.
Here r and c denote the row and column dimension
of the mesh of nodes encoded in the PLAPACK base communicator.
We will call this the
template vector.
In our discussion, we will start our indexing at zero, as is
customary in C.
PLAPACK allows one to specify whether
to start counting at one, as is customary in FORTRAN, or zero.
,
as illustrated in Figure 2.1.
Here r and c denote the row and column dimension
of the mesh of nodes encoded in the PLAPACK base communicator.
We will call this the
template vector.
In our discussion, we will start our indexing at zero, as is
customary in C.
PLAPACK allows one to specify whether
to start counting at one, as is customary in FORTRAN, or zero.
A distributed vector is aligned to this template vector by indicating the element of the template vector with which the first element of the vector to be distributed is aligned, as illustrated in Figure 2.1. The distribution of the elements of the vector to be distributed is then dictated by the distribution of corresponding elements of the template vector. Thus, if the first element of the vector is aligned with element i of the template vector, the j th element of the vector to be distributed is assigned to the same node as the i+j th element of the template vector.
The distribution of matrices is now induced by this template vector. More specifically, let T be an infinite matrix, partitioned like
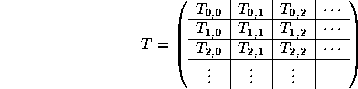
where ![]() are
are ![]() sub-matrices.
Then this
template matrix
is distributed to
nodes as induced by the template vector, t ,
as illustrated
in Figure
sub-matrices.
Then this
template matrix
is distributed to
nodes as induced by the template vector, t ,
as illustrated
in Figure ![]() .
A given matrix to be distributed is now
aligned to
this template by indicating the element of T with
which the top-left element of the matrix to be distributed
is aligned, as illustrated in Figure 2.2.
.
A given matrix to be distributed is now
aligned to
this template by indicating the element of T with
which the top-left element of the matrix to be distributed
is aligned, as illustrated in Figure 2.2.