John Gunnels
Calvin Lin
Greg Morrow
Robert van de Geijn
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712
{gunnels,lin,morrow,rvdg}@cs.utexas.edu
A Technical Paper Submitted to IPPS 98
Publications concerning parallel implementation of matrix-matrix multiplication continue to appear with some regularity. It may seem odd that an algorithm that can be expressed as one statement and three nested loops deserves this much attention. This paper provides some insights as to why this problem is complex: Practical algorithms that use matrix multiplication tend to use different shaped matrices, and the shape of the matrices can significantly impact the performance of matrix multiplication. We provide theoretical analysis and experimental results to explain the differences in performance achieved when these algorithms are applied to differently shaped matrices. This analysis sets the stage for hybrid algorithms which choose between the algorithms based on the shapes of the matrices involved. While the paper resolves a number of issues, it concludes with discussion of a number of directions yet to be pursued.
Over the last three decades, a number of different approaches have been proposed for implementation of matrix-matrix multiplication on distributed memory architectures. These include Cannon's algorithm [7], the broadcast-multiply-roll algorithm [16, 15], and Parallel Universal Matrix Multiplication Algorithm (PUMMA) [11]. This last algorithm is a generalization of broadcast-multiply-roll to non-square meshes of processors. An alternative generalization of this algorithm [19, 20] and an interesting algorithm based on a three-dimensional data distribution have also been developed [2].
The approach now considered the most practical,
sometimes known as broadcast-broadcast, was first proposed by Agarwal
et al. [1], who showed that a sequence of parallel rank-k
(panel-panel) updates is a highly effective way to parallelize C = A B .
That same observation was independently made by van de Geijn et
al. [24], who introduced the Scalable Universal Matrix Multiplication
Algorithm (SUMMA). In addition to computing C = A B as a sequence
of panel-panel updates, SUMMA implements 
and 
as a sequence of matrix-panel (of vectors) multiplications,
and 
as a sequence of panel-panel
updates. Later work [8] showed how these techniques can be
extended to a large class of commonly used matrix-matrix operations that are
part of the Level-3 Basic Linear Algebra Subprograms [12].
All of the efforts above-mentioned have concentrated primarily on the special case where the input matrices are approximately square. More recently, work by Li, et al. [22] attempts to create a ``poly-algorithm'' that chooses between three of the above algorithms (Cannon's, broadcast-multiply-roll, and broadcast-broadcast). Through empirical data they show some advantage when meshes are non-square or odd shaped. However, the algorithms being considered are not inherently more adapted to specific shapes of matrices, and thus limited benefit is observed.
In earlier work [23, 4, 3] we observe the need for algorithms to be sensitive to the shape of the matrices, and we hint at the fact that a class of algorithms naturally supported by the Parallel Linear Algebra Package (PLAPACK) infrastructure provides a convenient set of algorithms to serve as the basis for such shape-adaptive algorithms. Thus, a number of hybrid algorithms are now part of PLAPACK. This observation was also made as part of the ScaLAPACK [9] project, and indeed ScaLAPACK includes a number of matrix-matrix operations that are implemented to choose algorithms based on the shape of the matrix. We comment on the difference between our approach and ScaLAPACK later.
This paper provides a description and analysis of the class of parallel matrix multiplication algorithms that naturally lends itself to hybridization. The analysis combines theoretical results with empirical results to provide a complete picture of the benefits of the different algorithms and how they can be combined into hybrid algorithms. A number of simplifications are made to provide a clear picture that illustrates the issues. Having done so, a number of extensions are identified for further study.
For our analysis, we will assume a logical 
mesh of
computational nodes which are indexed 
, 
and 
, so that the total number of nodes is p = r c .
These nodes are connected through some communication network, which could be
a hypercube (Intel iPSC/860), a higher dimensional mesh (Intel Paragon, Cray
T3D/E) or a multistage network (IBM SP2).
We will assume that in the absence of network conflict, sending a message of length n between any two nodes can be modeled by
where 
represents the latency (startup cost) and 
the cost
per byte transferred. For all available communication networks, the
collective communications in Section 2.2.2 can be implemented to
avoid network conflicts. This will in some networks require an increased
number of messages, which affects the latency incurred.
In the matrix-matrix multiplication algorithms discussed here, all communication encountered is collective in nature. These collective communications are summarized in Table 1.
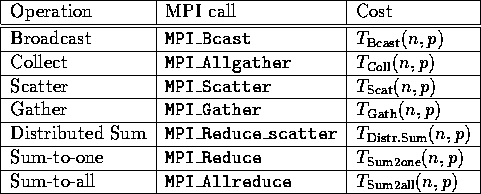
Table 1: Collective communication routines used in matrix-matrix
multiplication.
Frequently operations like broadcast are implemented
using minimum spanning trees, in which case the
cost can be modeled by
.
However, when n is large, better algorithms are available.
Details on the algorithms and estimated costs can be found
in the literature (e.g., [6, 15, 18]).
All computation on the individual nodes will be implemented using calls to
highly optimized sequential matrix-matrix multiply kernels that are part of
the Level-3 Basic Linear Algebra Subprograms (BLAS) [12]. In our
model, we will represent the cost of one add or one multiply by 
.
For many vendors, the shape of the matrices involved in a sequential matrix-matrix multiply (dgemm call) influences the performance of this kernel. Given the operation
there are three dimensions: m , n , and k, where C is 
, A is 
and B is 
. In a typical use,
each of these dimensions can be either large or small, leading to the
different shapes given in Table 2. In our model, we will use
a different cost for each shape, as indicated in the table. The fact that
this cost can vary considerably will be demonstrated in
Section 4 and Table 5.
We identify the different shapes by the operation they become when ``small''
equals one, which indicates that one or more of the matrices become scalars
or vectors. The different operations gemm, gemv, ger,
axpy, and dot refer to the BLAS routines
for
neral atrix-atrix multiplication,
atrix-ector multiplication, ank-1
update,
scalar--times--lus-, and
product. The names for some of the cases reported in the
last column come from recognizing that when ``small'' is greater than one
but small, a
matrix that has a row or column dimension of one becomes a row panel or
column panel of vectors, respectively.
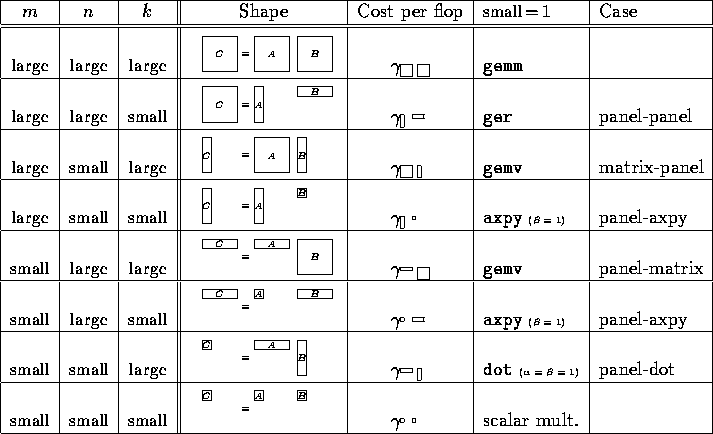
Table 2: Different possible cases for C = A B .
We have previously observed [14] that data distributions should focus on the decomposition of the physical problem to be solved, rather than on the decomposition of matrices. Typically, it is the elements of vectors that are associated with data of physical significance, and it is therefore their distribution to nodes that is significant. A matrix, which is a discretized operator, merely represents the relation between two vectors, which are discretized spaces: y = A x . Since it is more natural to start by distributing the problem to nodes, we partition x and y , and assign portions of these vectors to nodes. The matrix A is then distributed to nodes so that it is consistent with the distribution of the vectors, as we describe below. We call such matrix distributions physically based if the layout of the vectors which induce the distribution of A to nodes is consistent with where an application would naturally want them. We will use the abbreviation PBMD for Physically Based Matrix Distribution.
We now describe the distribution of the vectors, x and y , to nodes,
after which we will show how the matrix distribution is induced
(derived) by this vector distribution.
Let us assume x and y are of length n and m , respectively.
We will distribute these vectors using a distribution block size
of 
.
For simplicity assume 
and 
.
Partition x and y so that
where N >> p and M >> p
and each 
and 
is of length .
Partitioning A conformally yields
the blocked matrix
where each subblock is of size 
.
Blocks of x and y onto a two-dimensional
mesh of nodes in column-major order, as illustrated in Fig. 1.
The matrix distribution is induced by these vector distributions by
assigning blocks of columns 
to the same column of nodes as subvector 
, and blocks of
rows 
to the same row of nodes as subvector .
This is illustrated in Fig. 1, taken from [23].
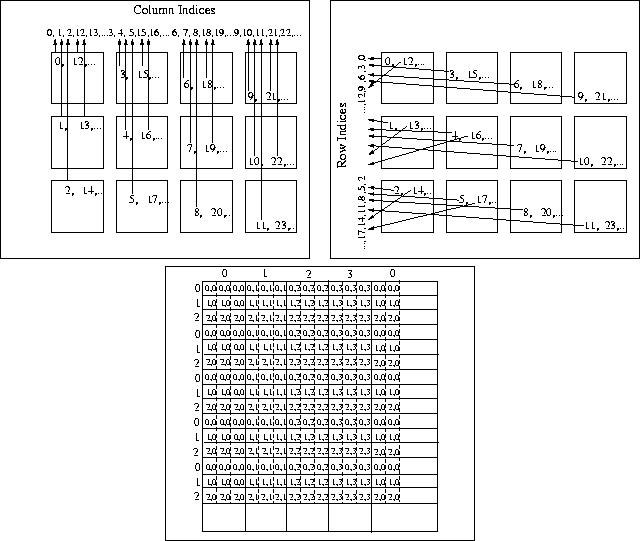
Figure 1:
Inducing a matrix distribution from vector distributions
when the vectors are over-decomposed.
Top: The subvectors of x and y are assigned
to a logical 
mesh of nodes by wrapping in column-major
order.
By projecting the indices of y to the left,
we determine the distribution of the matrix row-blocks of A .
By projecting the indices of x to the top,
we determine the distribution of the matrix column-blocks of A .
Bottom: Distribution
of the subblocks of A .
The indices indicate
the node to which the subblock is mapped.
Notice that the distribution of the matrix wraps blocks of rows and columns onto rows and columns of processors, respectively. The wrapping is necessary to improve load balance.
As part of our cost analysis in the subsequent sections, it will be important to compute the maximum number of elements of a vector x of length n assigned to a processor. Similarly, we need the maximum number of matrix elements assigned to any node. Functions for these quantities are given in Table 3.
Table 3: Functions that give the maximum local number of elements
for distributed vectors and matrices.
In the PBMD representation, vectors are fully distributed (not duplicated!),
while a single row or column of a matrix will reside in a single row or
column of processors. One benefit of the PBMD representation is the clean
manner in which vectors, matrix rows, and matrix columns interact.
Redistributing a column of a matrix like a vector requires a scatter
communication within rows. The natural extension is that redistributing a
panel of columns like a multivector (a group of vectors) requires each of the
columns of the panel to be scattered within rows. In
Table 4, we show the natural data movements encountered
during matrix-matrix multiplication, and their costs.
In that table, we also count the time for packing ( 
) and unpacking ( 
)
data into a format that allows for the collective communication to
proceed.
The necessity for this can be seen by carefully examining Fig. 1, which shows that when indices that indicate vector distribution
are projected to derive row and column distribution, an interleaving
occurs.
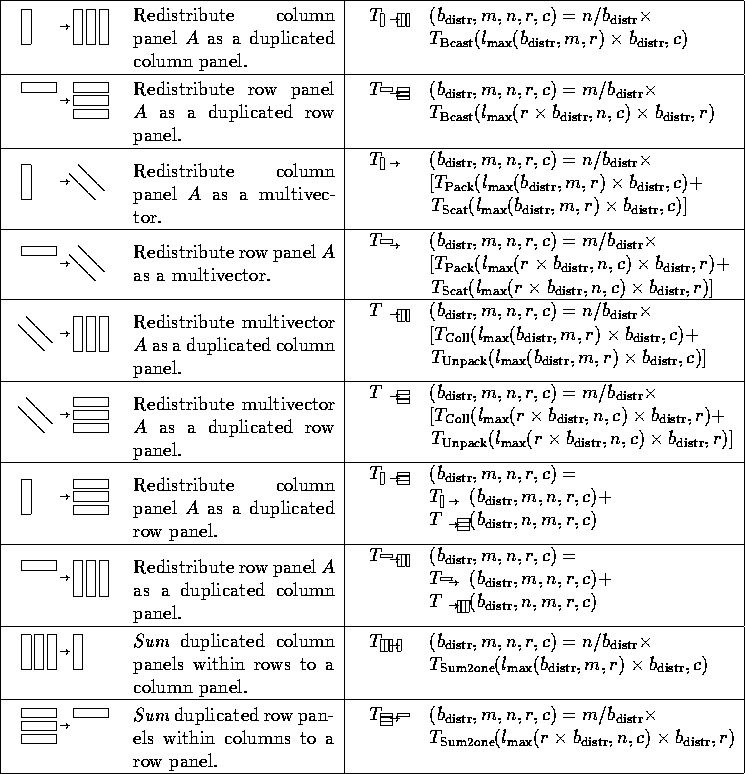
Table 4: Data movements encountered as part of matrix-matrix
multiplication.
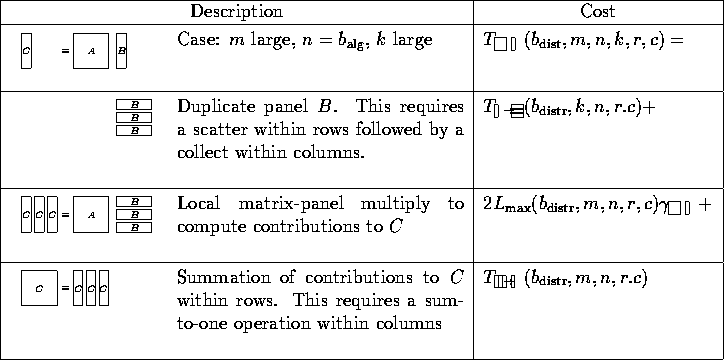
The previous section laid the foundation for the analysis of a class of parallel matrix-matrix multiplication algorithms. We show that different blockings of the operands lead to different algorithms, each of which can be built from a simple parallel matrix-matrix multiplication kernel. These kernels themselves can be recognized as the special cases in Table 2 where one or more of the dimensions are small.
The kernels can be separated into two groups. For the first, at least two
dimensions are large, leading to operations involving matrices and
panels of rows or columns: the panel-panel
update,
matrix-panel multiply, and panel-matrix multiply. Notice that these cases
are similar to kernels used in our paper [8] for parallel
implementation of matrix-matrix operations as well as basic building blocks
used by ScaLAPACK for parallel implementation of Basic Linear Algebra
Subprograms. However, it is the systematic data movement supported by
PLAPACK that allows the straight-forward implementation, explanation and
analysis of these operations, which we present in the rest of this section.
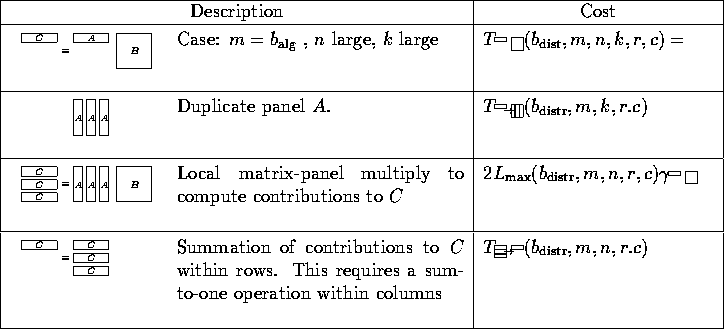
The second group of kernels assumes that only one of the dimensions is large, making one the operands a small matrix, and the other two row or column panels. Their implementation recognizes that when the bulk of the computation involves operands that are panels, redistributing like a multivector becomes beneficial. These kernels inherently can not be supported by ScaLAPACK due to fundamental design decisions underlying that package. In contrast, Physically Based Matrix Distribution and PLAPACK naturally support their implementation.
We will see that all algorithms will be implemented as a series of calls to these kernels. One benefit from this approach is that a high level of performance is achieved while workspace required for storing duplicates of data is kept reasonable.
We recognize that due to page limitations, the explanations of the algorithms are somewhat terse. We refer the reader to the literature [8, 23, 24] for additional details.
For simplicity, we will assume that the dimensions m , n , and k
are integer multiples of the algorithmic block size 
.
When discussing these algorithms, we will use the following partitionings
of matrices A , B , and C :
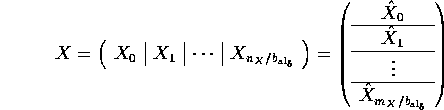
where 
, and 
and 
are
the row and column dimension of the indicated matrix.
Also,
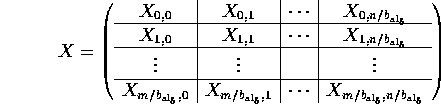
In the above partitionings, the block size is
choosen to maximize the performance of the local matrix-matrix
multiplication operation.
Observe that
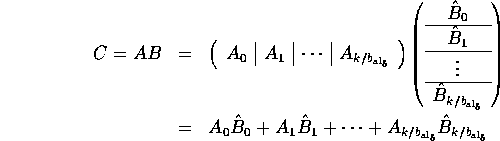
Thus, matrix-matrix multiplication can be implemented
as 
calls to a kernel that performs a
panel-panel multiplication. This kernel can be
implemented as follows:
The cost of calling this kernel repeatedly to compute C = A B becomes
Observe that
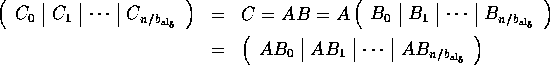
Thus, matrix-matrix multiplication can be
implemented by computing each column panel of C, 
,
by a call to a matrix-panel kernel:
The total cost to compute C = A B in this fashion is
Observe that
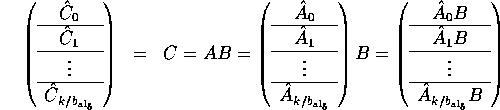
Thus, matrix-matrix multiplication can be
implemented by computing each row panel of C, 
,
by a call to the panel-matrix kernel:
The total cost is given by
Observe that
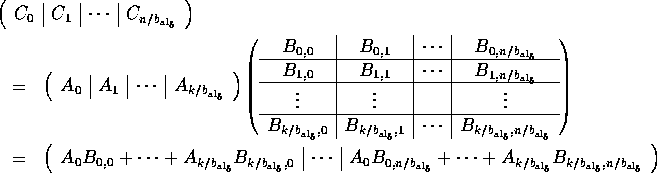
Thus, each column panel of C, , can
be computed by calls to the panel-axpy kernel:
For computing all panels in this fashion, the cost becomes
Alternatively, C and B can be partitioned by row blocks,
and A into blocks,
which leads to an algorithm that computes each row panel
of C by
calls to an alternative panel-axpy kernel.
This leads to a total cost of
Observe that
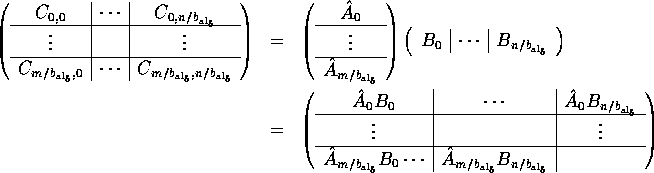
Thus, each block 
can be computed as a panel-dot operation:
Total cost:
In this section, we report preliminary performance results on the Cray T3E of implementations of the described algorithms. Our implementations were coded using the PLAPACK library infrastructure, which naturally supports these kinds of algorithms. In addition, we report results from our performance model.
In order to report results from our performance model, a number of parameters must first be determined. These can be grouped onto two sets: communication related parameters and computation related parameters.
All PLAPACK communication is accomplished by calls to the Message-Passing
Interface (MPI).
Independent of the algorithms, we determined the communication related
parameters by performing a simple "bounce-back" communication.
From this, the latency (or startup cost) was measured to equal
sec. while the cost per byte communicated equaled
nanosec. (for a transfer rate of 22 Mbytes per second).
For the data movements that require packing, we measured cost
per byte packed to be
nanosec.
Considerable improvements in the PLAPACK packing routines
can still be achieved and thus we expect this overhead to be
reduced in the future.
Ultimately, it is the performance of the local 64 bit matrix-matrix multiplication implementation that determines the asymptotic performance rate that can be achieved. Notice that our algorithms inherently operate on matrices and panels, and thus the performance for the different cases in Table 2 where "small" is taken to equal the algorithmic blocking size needs to be determined. In our preliminary performance tests, we chose the algorithmic blocking size to equal 128, which has, in the past, given us reasonable performance for a wide range of algorithms. Given this blocking size, the performance of the local BLAS matrix-matrix multiplication kernel is given in Table 5.
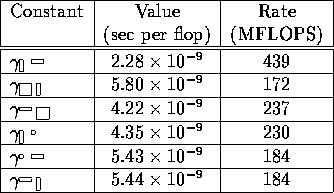
Table 5: Values of the local computational parameters measured
on the Cray T3E. Notice, these parameters represent performance
of an early version of the BLAS.
It is interesting to note that it is the panel-panel kernel that performs best. To those of us experienced with high-performance architectures this is not a surprise: This is the case that is heavily used by the LINPACK benchmark, and thus the first to be fully optimized. There is really no technical reason why for a block size of 128 the other shapes do not perform equally well. Indeed, as an architecture matures, those cases also get optimized. For example, on the Cray T3D the performance of the local matrix-matrix BLAS kernel is not nearly as dependent on the shape.
In this section, we demonstrate both through the cost model and measured data how the different algorithms perform as a function of shape. To do so, we fix one or two of the dimensions to be large and vary the other dimension(s).
In Figure 2, we show the predicted and measured performance of the various algorithms when both m and n are fixed to be large.
First, let us comment on the asymptotic behavior.
It is the case that for the panel-panel, matrix-panel, and panel-matrix
algorithms as k gets large, communication and other overhead
eventually become a lower order term when compared to computation.
Thus, asymptotically, they should all approach a performance rate
equal to the rate achieved by the local matrix-matrix kernel.
This argument does not hold for the panel-axpy and panel-dot
based algorithms: For each call the the parallel panel-axpy and
panel-dot kernel, 
or 
data is communicated before performing
floating point operations. Thus,
if , r and c are fixed, communication
does not become less significant, even if the matrix dimensions
are increased.
All of these observations can be observed in the graphs.
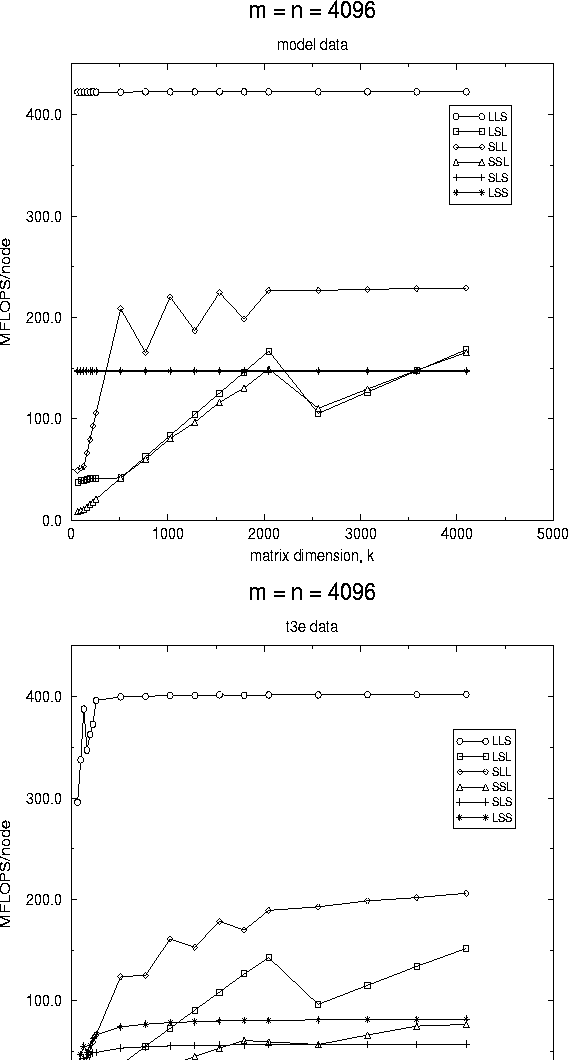
Figure 2: Performance of the various algorithms on a
16 processor configuration of the Cray T3E.
In this graph, two dimensions, m and n are fixed to be large,
while k is varied.
A distribution block size equal to the
algorithmic block size of 128 was used to collect this data.
The graph on the left reports data derived from the model, while
the graph on the right reports measured data.
Next, notice from the graphs that the panel-panel based algorithm always outperforms the others. A moment of thought leads us to conclude that this is natural, since the panel-panel kernel is inherently designed for the case where m and n are large, and k is small. By comparison, a matrix-panel based algorithm will inherently perform badly when k is small, since in that algorithm parallelism is derived from the distribution of A , which is only distributed to one or a few columns of nodes when k is small. Similar arguments explain the poor behavior of the other algorithms when k is small.
Finally, comparing the graph derived from the model to the graph reporting measured data, we notice that while the model is clearly not perfect, it does capture qualitatively the measured data. Also, the predicted performance reasonably reflects the measured performance, especially for the panel-panel, matrix-panel, and panel-matrix based algorithms.
In Fig. 3, we show the predicted and measured performance of the various algorithms when both m and k are fixed to be large.
Again, we start by commenting on the asymptotic behavior. As for the case where m and k are fixed to be large, for the panel-panel, matrix-panel, and panel-matrix algorithms as k gets large, communication and other overhead eventually become a lower order term when compared to computation. Thus, asymptotically, they should and do all approach a performance rate equal to the rate achieved by the local matrix-matrix kernel. Again, this argument does not hold for the panel-axpy and panel-dot based algorithms. All of these observations can be observed in the graphs.
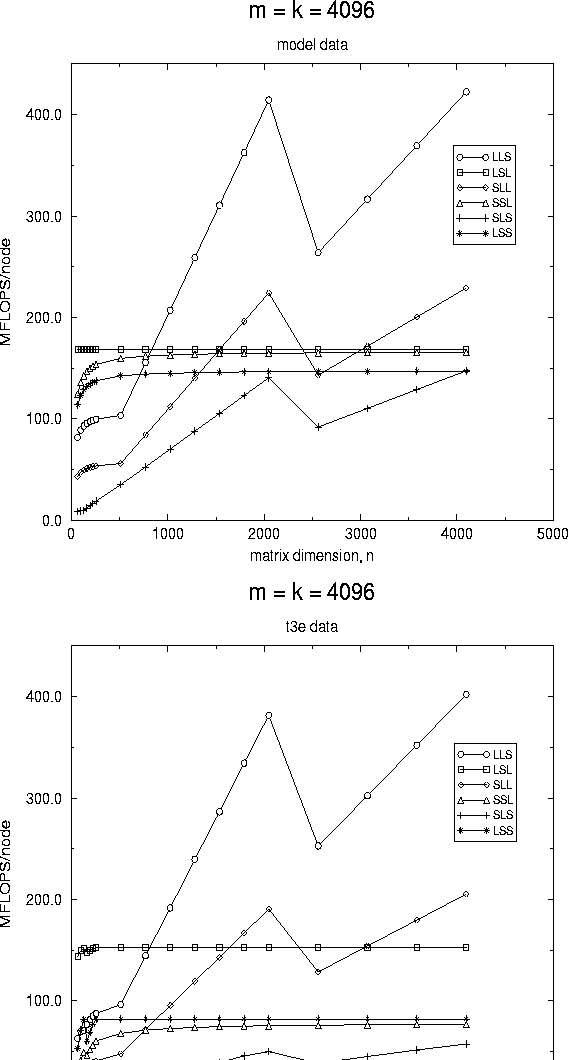
Figure 3: Performance of the various algorithms on a
16 processor configuration of the Cray T3E.
In this graph, two dimensions, m and k are fixed to be large,
while n is varied.
A distribution block size equal to the
algorithmic block size of 128 was used to collect this data.
The graph on the left reports data derived from the model, while
the graph on the right reports measured data.
Next, notice from the graphs that the matrix-panel based algorithm initially outperforms the others. This is natural, since the matrix-panel kernel is inherently designed for the case where m and k are large, and n is small. By comparison, a panel-panel or panel-matrix based algorithm will inherently perform badly when n is small, since in those algorithms parallelism is derived from the distribution of C and B , respectively, which are only distributed to one or a few columns of nodes when k is small. Similar arguments explain the poor behavior of the other algorithms when k is small.
Notice that eventually the panel-panel based algorithm outperforms the matrix-panel algorithm. This is solely due to the fact that the implementation of the local matrix-matrix multiply is more efficient for the panel-panel case.
Again,the model is clearly not perfect, but does capture qualitatively the measured data. For the panel-panel, matrix-panel and panel-matrix based algorithms, the model is quite good: for example, it predicts the cross-over point where the panel-panel algorithm becomes superior to within five percent.
In Fig. 4, we present results for one of the cases where only one dimension is fixed to be large. This time, we would expect one of the panel-axpy based algorithms to be superior, at least when the other dimensions are small. While it is clear from the graphs that the other algorithms perform poorly when m and k are small, due to time pressures, we did not collect data for the case where m and k were extremely small (much less than the algorithmic blocking size) and thus at this moment we must declare the evidence inconclusive.
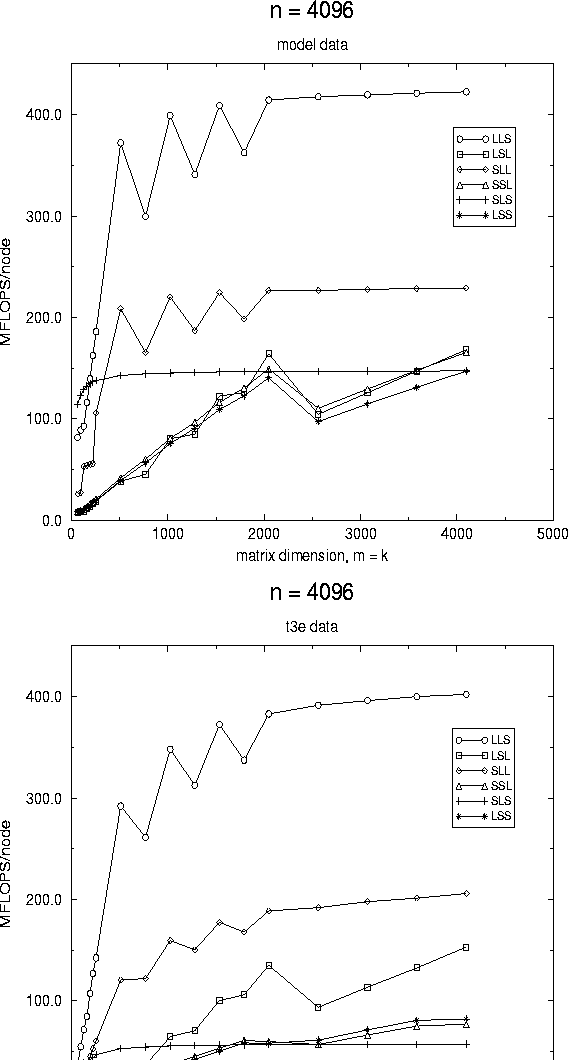
Figure 4: Performance of the various algorithms on a
16 processor configuration of the Cray T3E.
In this graph, one dimension, n is fixed to be large
and m = k are varied.
A distribution block size equal to the
algorithmic block size of 128 was used to collect this data.
The graph on the left reports data derived from the model, while
the graph on the right reports measured data.
In this paper, we have systematically presented algorithms, analysis, and performance results for a class of parallel matrix algorithms. This class of algorithms allows for high performance to be attained across a range of shapes of matrices.
As mentioned, the results presented in the previous section are extremely preliminary. They are literally the first results computed with the model and the first results for implementations of the panel-axpy and panel-dot based algorithms.
The good news is that certainly qualitatively the model reflects the measured performance. Even quantitatively, the initial results look good. Finally, there were no surprises: both the model and the empirical results reflected what we expected from experience.
A lot of further experimentation must and will be performed in order to paint a complete picture:
We conclude by remarking that if the model were perfect, it could be used to pick between the different algorithms, thus creating a hybrid algorithm. Clearly, too many unknown parameters make it difficult to tune the model for different vendors. Thus there is a need for simple heuristics which are not as sensitive to imperfections in the model. If the vendors supplied local matrix-matrix multiply kernels that performed reasonably well for all shapes of matrices encountered in this paper, this task would be greatly simplified. In particular, choosing between the algorithms that target the case where at least two dimensions are large would become a matter of determining which matrix has the largest number of elements. The algorithm that keeps that matrix stationary, communicating data from the other matrices, should perform best, since parallelism is derived from the distribution of that stationary matrix. Similarly, choosing between the algorithms that target the case where at one dimension is large would become a matter of determining which matrix has the least number of elements. The algorithm that redistributes the other two matrices should perform best, since parallelism is derived from the length of the matrices that are redistributed. Thus, what would be left would be to determine whether shapes of the matrices are such that at least two dimensions are large, or only one dimension is large. Investigation of this heuristic is left as future research.
We are indebted to the rest of the PLAPACK team (Philip Alpatov, Dr. Greg Baker, Dr. Carter Edwards, James Overfelt, and Dr. Yuan-Jye Jason Wu) for providing the infrastructure that made this research possible.
Primary support for this project come from the Parallel Research on Invariant Subspace Methods (PRISM) project (ARPA grant P-95006) and the Environmental Molecular Sciences construction project at Pacific Northwest National Laboratory (PNNL) (PNNL is a multiprogram national laboratory operated by Battelle Memorial Institute for the U.S. Department of Energy under Contract DE-AC06-76RLO 1830). Additional support for PLAPACK came from the NASA High Performance Computing and Communications Program's Earth and Space Sciences Project (NRA Grants NAG5-2497 and NAG5-2511), and the Intel Research Council.
We gratefully acknowledge access to equipment provided by the National Partnership for Advanced Computational Infrastructure (NPACI), The University of Texas Computation Center's High Performance Computing Facility, and the Texas Institute for Computational and Applied Mathematics' Distributed Computing Laboratory,
For additional information, visit the PLAPACK web site: http://www.cs.utexas.edu/users/plapack
Analysis of a
Class of
Parallel Matrix Multiplication
Algorithms
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 -link 1 -show_section_numbers -address rvdg@cs.utexas.edu ipps97.tex.
The translation was initiated by Robert van de Geijn on Thu Oct 30 16:33:53 CST 1997
