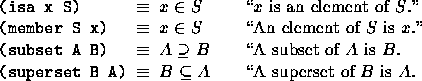
The basic structure of the knowledge base is organized around sets, their elements, and their subsets.
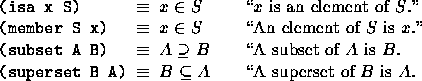
Knowledge representation in Algernon exploits access limitations, so an individual will normally be linked explicitly to some of its containing sets, but most large sets will not be explicitly linked to their members.
The taxonomy of fundamental objects is set up as follows:
(:taxonomy (things
(rules)
(objects
(sets things objects sets slots)
(booleans true false :complete)
(contexts global-context))
(slots
(order-relations
(tc-order-relations
(equivalence-relations))))))
Every frame in the knowledge-base is a member of the set things, which breaks down into the sets objects and slots, and so on. In the knowledge-base, the taxonomy is represented using isa and superset relations (and their inverses member and subset ). isa links an object to a set of which it is a member, and superset links a set to a superset of it (thus member links a set to one of its members, and subset links a set to one of its subsets).
A basic design decision in building large taxonomies is whether to link an object in the taxonomy to every set it is a member of, to link it to just the `lowest' set in the taxonomy it is a member of (and then link this set up to the sets higher up in the taxonomy using superset links), or to link it to some of the sets it is a member of. We have chosen to take the third course, and link objects to just the ``important'' sets they are a member of. This distinction is represented using the relations superset and imp-superset. Intuitively, imp-superset links a set to an `important' superset. Operationally this means that if Algernon learns that an object, x is a member of a set s, and s has an important superset S, then a forward-chaining rule immediately adds an isa link between x and S.
(:rules things ((isa ?x ?s1) (imp-superset ?s1 ?s2) -> (isa ?x ?s2)))
The slot declarations for some of the important slots defined in the built-in knowledge-base are given below:
(:slot isa (things sets)
:comment "(isa ?x ?s) = ?x is a member of the set ?s.")
(:slot member (sets things)
:backlink isa
:comment "(member ?s ?x) = A member of ?s is ?x.")
(:slot subset (sets sets)
:comment "(subset ?s1 ?s2) = A subset of ?s1 is ?s2.")
(:slot superset (sets sets)
:inverse subset
:comment "(superset ?s1 ?s2) = A superset of ?s1 is ?s2.")
(:slot selfset (things sets)
:cardinality 1
:backlink member
:comment "The selfset of x is the set {x}.")
(:slot less (objects objects)
:comment "(less ?x ?y) = ?x less than ?y.")
(:slot greater (objects objects)
:inverse less
:comment "(greater ?x ?y) = ?x greater than ?y.")
(:slot equal (objects objects)
:inverse equal
:comment "(equal ?x ?y) = ?x is equal to ?y.")
(:slot least (objects sets)
:comment "(least ?x ?s) = ?x is the least member of ?s.")
(:slot greatest (objects sets)
:comment "(greatest ?x ?s) = ?x is the greatest member of ?s.")