Section 3.1 Opening Remarks
¶Unit 3.1.1 Launch
¶The current plan is to discuss the memory hierarchy and how MMM allows data movement to be amortized. Maybe the following can be the opener for Week 3:
The inconvenient truth is that floating point computations can be performed very fast while bringing data in from main memory is relatively slow. How slow? On a typical architecture it takes two orders of magnitude more time to bring a floating point number in from main memory than it takes to compute with it.
The reason why main memory is slow is relatively simple: there is not enough room on a chip for the large memories that we are accustomed to, and hence they are off chip. The mere distance creates a latency for retrieving the data. This could then be offset by retrieving a lot of data simultaneously. Unfortunately there are inherent bandwidth limitations: there are only so many pins that can connect the central processing unit with main memory.
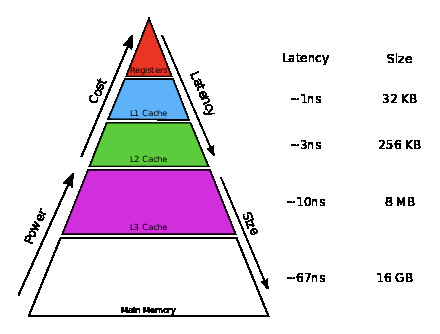
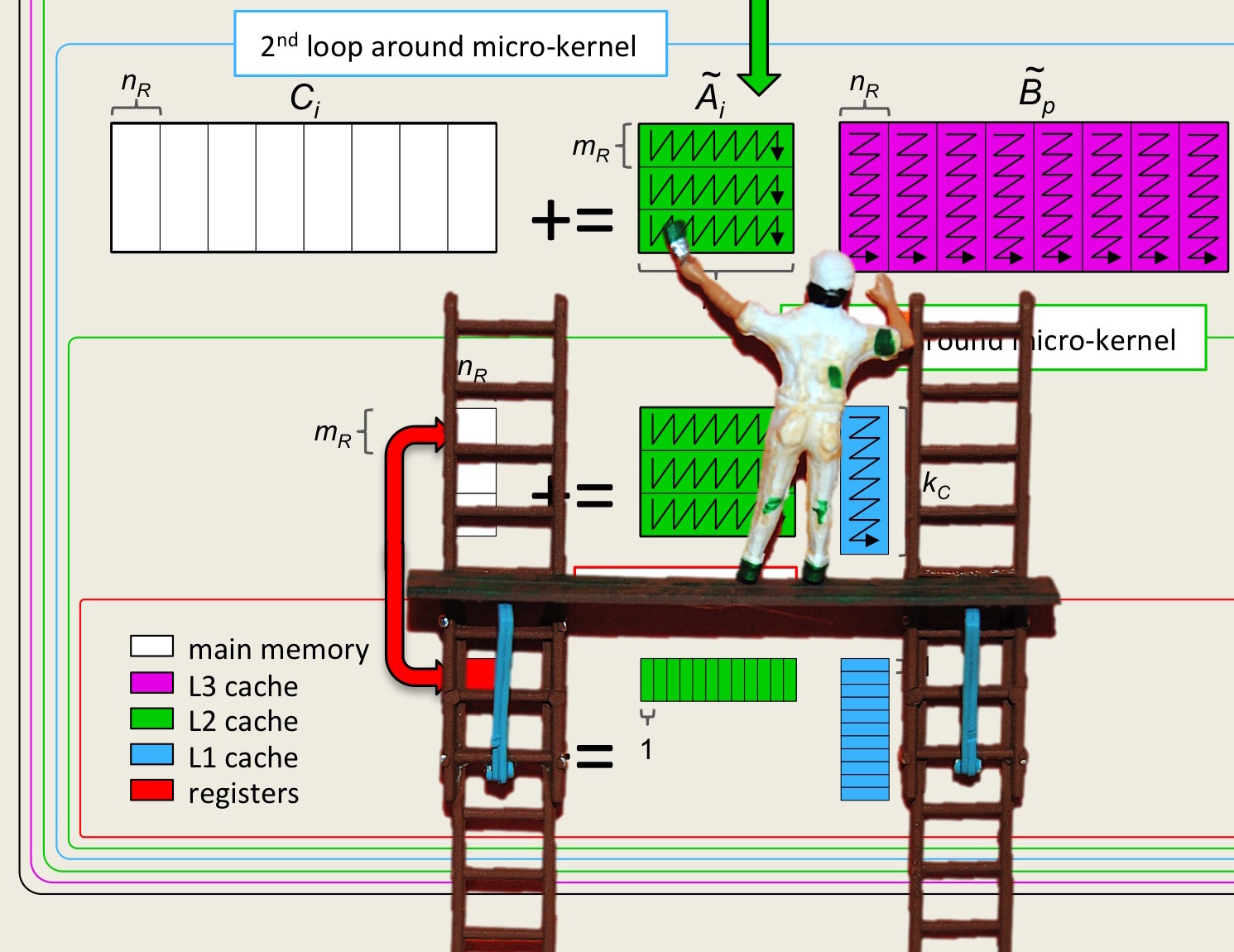
To overcome this limitation, a modern processor has a hierarchy of memories. We have already encountered the two extremes: registers and main memory. In between, there are smaller but faster {\em cache memories}. These cache memories are on-chip and hence do not carry the same latency as does main memory and also can achieve greater bandwidth. The hierarchical nature of these memories is often depicted as a pyramid as illustrated in Figure 3.1.1. To put things in perspective: We have discussed that the Haswell processor has sixteen vector processors that can store 64 double precision floating point numbers (doubles). Close to the CPU it has a 32Kbytes level-1 cache (L1 cache) that can thus store 4,096 doubles. Somewhat further it has a 256Kbytes level-2 cache (L2 cache) that can store 32,768 doubles. Further away yet, but still on chip, it has a 8Mbytes level-3 cache (L3 cache) that can hold 524,288 doubles.
Homework 3.1.3
Since we compute with (sub)matrices, it is useful to have some idea of how big of a matrix one can fit in each of the layers of cache. Assume each element in the matrix is a double precision number, which requires 8 bytes. Assume each element in the matrix is a double precision number, which requires 8 bytes.
\begin{equation*}
\begin{array}{| c | r | l |}\hline
{\rm Layer} \amp
{\rm Size} \amp
{\rm Largest~} n \times n {\rm ~matrix} \\ \hline
{\rm registers} \amp 16
\times 4 {\rm ~doubles} \amp
n = ~~~~~~~~~~~
\\ \hline
{\rm L1~cache}\amp 32 {\rm ~Kbytes} \amp
n = ~~~~~~~~~~~
\\ \hline
{\rm L2~cache} \amp 256 {\rm ~Kbytes} \amp
n = ~~~~~~~~~~~
\\ \hline
{\rm L3~cache} \amp 8 {\rm ~Mbytes} \amp
n = ~~~~~~~~~~~~~~~~~~~~~~
\\ \hline
\end{array}
\end{equation*}
(The cache sizes given here are for a Intel Haswell processor.)
Solution
\begin{equation*}
\begin{array}{| c | r | l |}\hline
{\rm Layer} \amp
{\rm Size} \amp
{\rm Largest~} n \times n {\rm ~matrix} \\ \hline
{\rm registers} \amp 16
\times 4 {\rm ~doubles} \amp
n = \sqrt{ 64 } = 8
\\ \hline
{\rm L1~cache}\amp 32 {\rm ~Kbytes} \amp
n = \sqrt{32 \times 1024 / 8} = 64
\\ \hline
{\rm L2~cache} \amp 256 {\rm ~Kbytes} \amp
n = \sqrt{ 256 \times 1024 / 8 } = 181
\\ \hline
{\rm L3~cache} \amp 8 {\rm ~Mbytes} \amp
n = \sqrt{ 8 \times 1024 \times 1024/ 8 } = 1024
\\ \hline
\end{array}
\end{equation*}
Unit 3.1.2 Outline Week 3
¶Under construction.
Unit 3.1.3 What you should know
¶Under construction