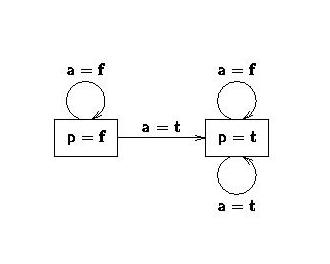
We will refer to this transition system as TS1. Its two edges labeled a=t represent the events in which action a is executed; these edges lead to the state p=t. The other two edges are labeled a=f (action a is not executed), so that these edges are loops.
If a system involves several fluents p1, p2, p3, ... then every vertex is labeled by a set of equations specifying the values of all fluents in the corresponding state, for instance:
If there are several actions a1, a2, a3, ... then every edge is labeled by a set of equations specifying which actions are executed in the corresponding event, for instance:
Assigning the value t to several action symbols indicates that the corresponding actions are executed concurrently.
Besides Boolean-valued fluents, transition systems may include fluents with
any other values. Consider, for instance, a fluent c that takes values
from an initial segment of nonnegative integers {0,...,N}. Transition
system TS2 below shows the effect of the action a that increments
c by 1 when c<N and is nonexecutable otherwise.
