Generalizing an old formula
It all started with a discussion about the role of pictures as substitute for calculational proofs. I was reminded of the pictorial illustration of the theorem that the sum of the first n odd natural numbers equals n2:
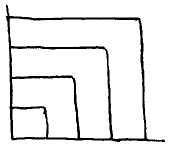
Immediately the question rose whether this formula can be generalized to higher powers of n, since from the 4th power onwards, visualization breaks down.
By mentally cutting 3 mutually orthogonal slices of thickness 1 from a cube of n by n by n , one can convince oneself that
| n3 = (S i: 1 ≤ i ≤ n: i2 + i·(i-1) + (i-1)2) |
and one begins to suspect the validity of
| n4 = (S i: 1 ≤ i ≤ n: i3 + i2·(i-1) + i·(i-1)2 + (i-1)3) |
and similar formula, in general
| nk = (S i: 1 ≤ i ≤ n: (S j: 0 ≤ j < k: ik-1-j·(i-1)j)). | (0) |
This holds provided
| nk = (S j: 0 ≤ j < k: nk-1-j·(n-1)j) + (n-1)k | (1) |
because (0) holds for n=0 , while (1) then provides the step for proving (0) by induction over n .
We prove (1), which holds for k=1 , by mathematical induction over k:
nk = (S j: 0 ≤ j < k: nk-1-j·(n-1)j) + (n-1)k
≡ { multiply both sides by n; n = 1 + (n-1) }
nk+1 = (S j: 0 ≤ j < k: nk-j·(n-1)j) + (n-1)k + (n-1)k+1
≡ { definition of summation and n0 = 1 }
nk+1 = (S j: 0 ≤ j < k+1: nk+1-1-j·(n-1)j) + (n-1)k+1
q.e.d.
The above was just for the record. I find the above double induction satisfactory and formula (0) was new for me.
Observation. In the mean time I asked people from five different countries: none of them had seen the above picture at school. We all agreed that that was a pity. (End of Observation)