On the theorem of Pythagoras

For the theorem of Pythagoras, I start from Coxeter's formulation ("Introduction to Geometry", p.8)

"In a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the two catheti."

Let us play a little bit with that formulation. In a triangle with sides a, b, and c —different from 0 so as to make its angles well-defined— we introdue the usual nomenclature α, β, and γ for their respective opposite angles. (We introduced one angle name so as to be able to express right-angledness, and the other two for reasons of symmetry.)

A formal expression of Coxeter's formulation is

γ = π/2     ⇒     a2 + b2 = c2     .

Besides the nomenclature we introduced, this formulation contains the (transcendantal!) constant π. Fortunately we can eliminate it thanks to

π = α + β +γ     .
Elementary arithmetic yields the equivalent formulation
α + β = γ     ⇒     a2 + b2 = c2     .
Isn't that nicely symmetric? It immediately suggests —at least to me— the strengthening

(0)      α + β = γ     ≡     a2 + b2 = c2     .

(This will turn out to be a theorem.) We get an equivalent formulation by negating both sides:
α + β ≠ γ     ≡     a2 + b2 ≠ c2     .

But x ≠ y   ≡   x < y   ∨   x > y , and the latter disjuncts are mutually exclusive. Remembering that the larger angle is opposite to the larger side, is it bold to guess

(1)      α + β < γ     ≡     a2 + b2 < c2                               and
(2)      α + β > γ     ≡     a2 + b2 > c2                  ?

Bold perhaps, but not unreasonable.

Note that (0), (1) and (2) are not independent: from any two of them, the third can be derived. They can be jointly formulated in terms of the function sgn —read "signum"— given by

sgn.0 = 0     ∧     (sgn.x =1   ≡   x > 0)     ∧     (sgn.x = -1   &equiv   x < 0) ,
viz.        sgn.(α + β - γ)    =    sgn.(a2 + b2 - c2)     .

Consider now the following figure. We have drawn
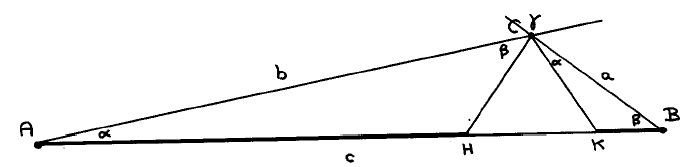
Image of Triangle

the case α + β < γ, in which the triangles ΔCKB and ΔAHC, of disjoint areas, don't cover the whole of ΔACB; denoting the area of ΔXYZ by "XYZ" we have in this case

CKB + AHC < ACB     .

In the case α + β = γ, H and K coincide and we have

CKB + AHC = ACB     ,
and in the case α + β > γ, the two triangles overlap and we have
CKB + AHC > ACB     .
In summary
sgn.(α + β - γ) = sgn.(CKB + AHC - ACB)     .

The three areas of the right-hand side are those of similar triangles and hence have the same ratios as the squares of corresponding lines, in particular

CKB/a2 = AHC/b2 = ACB/c2 > 0     ;
hence
sgn.(CKB + AHC - ACB) = sgn.(a2 + b2 - c2)     ,
Hence we have proved

sgn.(α + β - γ) = sgn.(a2 + b2 - c2)     ,

a theorem, say, 4 times as rich as the one we quoted from Coxeter.

*            *
*

The title of this note could make one wonder why I would waste my time flogging a horse as dead as Pythagoras's Theorem. So let us try to summarize what we could learn from this exercise.

•    Three cheers for formalization! Instead of setting out to prove a2 + b2 = c2 for a right-angled triangle, we included the antecedent γ = π/2 in the formal statement of what was to be proved. It was only after the introduction of π that we could eliminate it and met the "nicely symmetric" formulation.

•   Three cheers for the equivalence! It makes quite clear that the theorem is not about right-angled triangles, but about triangles in general.

•   Three cheers for the notational device captured in sgn. If we had not been careful, we would have ended up proving
(α + β) R γ    ≡    (a2 + b2) R c2
for R any of the six relations =, ≠, <, ≤, >, and ≥

•   No cheers at all for that stage of the argument in which lack of axiomatization forced us to resort to a picture. Pictures are almost unavoidably overspecific and therby often force a case analysis upon you. Note that I carefully avoided the pictures for α + β > γ; there are 9 of them: K to the right of A, coincident with A, and to the left of A, and similarly for the pair H and B. For the argument these distinctions are irrelevant but, when drawing a picture, you can hardly avoid making them.

•   One of these days I would like to find a convincing explanation of the circumstance that youngsters continue to be educated with the theorem of Pythagoras in its diluted form as quoted from Coxeter. Notice that the 9 figures could have been avoided by also proving
CKB + AHC < ACB      ⇒      α + β < γ          and
CKB + AHC = ACB      ⇒      &alpha + β = γ     ,
i.e. proving (0) and (1) in full.

•   Notice that our figure was not pulled out of a magicians hat! As soon as sgn.(α+β–γ) occurs in the demonstrandum, it is sweetly reasonable to construct that difference. In order not to destroy the symmetry between α and β, one starts with γ and subtracts α at the one side and β at the other:
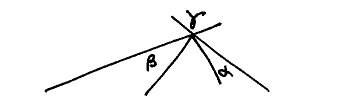
Looks like an American Indian Tepee
and this is the germ of the figure we drew.

Epilogue. I am in a paradoxical situation. I am convinced that of the people knowing the theorem of Pythagoras, almost no one can read the above without being surprised at least once. Furthermore, I think that all those surprises relevant (because telling about their education in reasoning). Yet I don't know of a single respectable journal in which I could flog this dead horse.

Austin, 7 September 1986

prof.dr.Edsger W.Dijkstra
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712-1188, USA
Transcription by Joel Hockey
Last revised on Thu, 27 May 2010.