Monochrome pairs in the three-coloured plane

A few months ago I encountered the following

Theorem   If each point in the Euclidean plane is red, white, or blue, there exists a monochrome pair of points with mutual distance 1.

This morning I looked at it again, and designed the following proof.

Consider the three-coloured plane. According to the pigeonhole principle, 4 points suffice to guarantee the existence of a monochrome pair among them. Regrettably, we cannot arrange them in such a way that all pairs are at distance 1. The best we can do is 5 pairs at distance 1 and 1 pair at distance √3:

          .

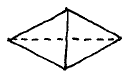Using the term “d-pair” to denote a pair of points with mutual distance d, we have to show: (there exists a monochrome 1-pair). The above configuration only allows us to conclude

Lemma	In the three-coloured plane
	(all √3-pairs are monochrome) ∨
	(there exists a monochrome 1-pair)

Consider now an isosceles triangle ABC.

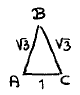
Then
      ¬ (there exists a monochrome 1-pair)
⇒       {Lemma}
      (all √3-pairs are monochrome)
⇒       {instantiation: AB and BC are √3-pairs}
      (AB and BC are monochrome)
⇒       {transitivity of equality}
      (AC is monochrome)
⇒       {instantiation: AC is a 1-pair}
      (there exists a monochrome 1-pair)   ,
and, since [¬P ⇒ P] ≡ [P], the above observation proves the theorem.

(End of Proof.)

^*         _*         ^*

When I encountered the theorem, I had convinced myself that the vertices of the complete triangular grid

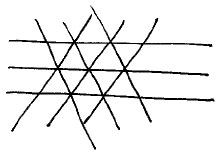  etc.

admit a three-colouring without monochrome neighbours. Consequently, I knew this morning that, of the Euclidean plane, something more than the existence of vertices of complete triangular grids had to be taken into account. (This turned out to be the existence of triangles of the shape of △ABC.)

We had to demonstrate the existence of monochrome 1-pairs. The above observation suggested the consideration of monochrome d-pairs with d≠1; that is how the monochrome √3-pairs entered the picture. The introduction of △ABC was then suggested by trying to exploit the meaning of the adjective “monochrome”, i.e., trying to exploit the properties of equality.

Nuenen, 18 June 1989

prof.dr. Edsger W.Dijkstra
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712-1188
USA.