Proving the theorem of Menelaos

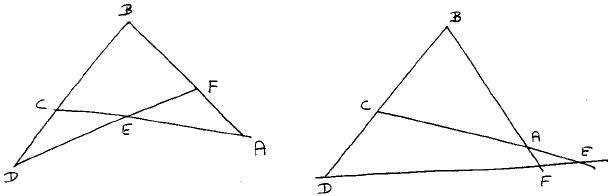
For non-degenerate triangle ABC and D, E, F collinear as in above figures the theorem of Menelaos states

BD ––– DC · CE ––– EA · AF ––– FB   =  –1       .

In terms of λ, μ, ν, defined by

D = λB + (1–λ)C,     E = μC + (1–μ)A,     F = νA + (1–ν)B

we have to conclude

1–λ ––– λ · 1–μ ––– μ · 1–ν ––– ν   =  –1       or

(0)	(1–λ) · (1–μ) · (1–ν) + λ·μ·ν = 0

from the fact that D, E, and F are collinear. This is expressed by

(1)	Det. P = 0   where   P =	Dx	Dy	1
		Ex	Ey	1
		Fx	Fy	1	.

Writing D_x = λB_x + (1–λ)C_x, etc. we can factorize   P = Q ·R   where

Q =	λ	1–λ	0		R =	Bx	By	1
	0	μ	1–μ			Cx	Cy	1
	1–ν	0	ν			Ax	Ay	1

From this factorization we conclude

(2)	Det. P = (Det. Q) · (Det. R)           .

Triangle ABC being non-degenerate is expressed by

(3)	Det. R ≠ 0           ,

and from (1), (2), (3) we conclude

Det. Q = 0           ,

which, in view of Q’s definition, equivales (0).

I designed the above proof in reaction to a very classical argument in which the above two figured had to be dealt with separately. I like the proof for the way R enters the picture. (And just in case you feel tempted to send me shorter proofs of Menelaos’s theorem: I know all about barycentric coordinates.)

Austin, 10 October 1990

prof.dr. Edsger W.Dijkstra
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712-1188
USA