Heuristics for a very simple Euclidean proof
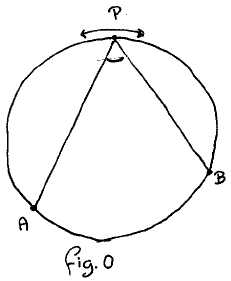
We consider 3 points on a given circle, A and B fixed and P movable along the clockwise circle segment from A to B. (See fig. 0) At my recent oral examinations “Mathematical Methodology”, the students I asked did not know the theorem that ∠APB is constant, i.e. independent of the position of P. So we designed the proof in as systematic a manner as possible.
* * *
• As a matter of routine we checked the relevance of the data. Is it essential that A is fixed? Yes, obviously. Is it essential that P is confined to the circle? Yes. (Some let ∠APB shrink by moving P outside the circle, some let it increase by moving P inside.) Moral: we have to take the circle into account.
• How is a circle defined? As a set of points equidistant to the centre. So we had better introduce the centre C and the three radii of equal length. (See fig. 1)
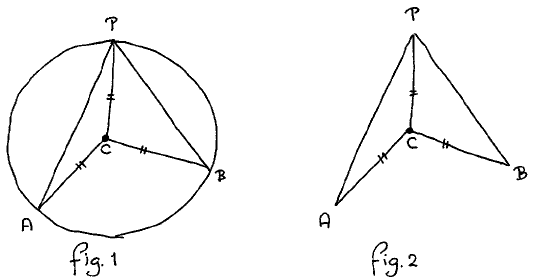
• Since it is only essential that A, B, and P lie on the circle and this fact has been captured, the circle is now erased. (See fig. 2)
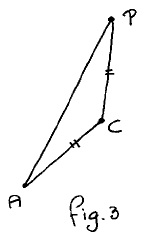
• Three distances are the same, but usually equality is considered to be a binary relation. If the fact that x, y, z are all equal has to be captured by the pairwise equalities x=y, y=z, z=x, then 2 of the 3 suffice (since = is transitive). Which of the two pairs should we choose in fig. 2? For reasons of symmetry these are AC=PC and BC=PC. Let us concentrate on the first one. (See fig. 3)
• What can we conclude from AC=PC? This was invariably the moment some mathematical knowledge was introduced: an isosceles triangle has equal base angles. Together with the other case this leads to fig. 4, in which equal angles have been marked equally.
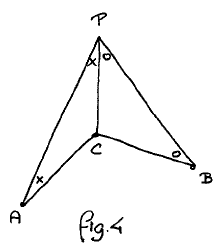
• At this stage, most students remarked without prompting that a vital step had been made: from a given in terms of lengths a conclusion about angles has to be drawn, and the last step is vital because it provides the transition from lengths to angles. This is the moment to decide to remove the markings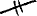 
of equal lengths and to conduct the remainder of the argument in terms of angles.
• We have to show that ∠APB is constant. We have not used yet that A, B, C, are fixed, and that therefore ∠ACB is constant. This observation draws our attention to the angles around C. (Had we not made this observation, we could have observed that the angles around C are in fig. 4 the only unmarked ones.) And this was the moment of the second introduction of some mathematical knowledge: most students chose to use that the angles of a triangle add up to π (which they called 180°). This leads to the marking as in fig. 5 and we conclude that ∠APB = ½ ∠ACB, which proves the theorem.
Note None of the students appealed to the theorem captured by
,
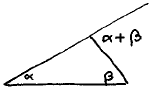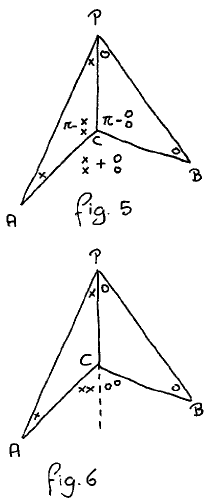
extended PC and produced the marking as in fig. 6. It has the advantage of not mentioning π*), and is suggested by the observation that, at P, we have a constant angle with a variable partitioning: by extending PC, we create another constant angle with variable partitioning.
*) The problem of introducing a constant (like π) is that then one has to use its properties. (End of Note.)
The problem was nice for warming up!
Winding Stairs Campground,
14 May 1994
prof.dr. Edsger W.Dijkstra
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712-1188