EWD 1194

Z.P.Su’s second problem

The other day Zhendong Patrick Su showed me the following problem of the last Putnam Competition, in which he had participated. (He had solved the problem, I did not.)

Consider the points in or on the right-angled triangle with hypotenuse of length √2:

EWD1194 figure 1.

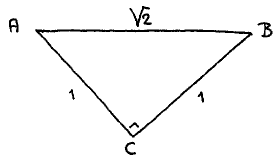Let each of these points have 1 of 4 colours. Show the existence of a monochrome pair with mutual distance ≥ 2 − √2.

Let us call that critical distance r, i.e. r = 2 − √2 ; let us call a monochrome pair at mutual distance ≥ r a “desired pair”.

If A belongs to a desired pair, we are done; similarly for B. If neither A nor B belongs to a desired pair, we proceed as follows.

To begin with we observe that r satisfies r = √2 · (1−r), from which we

EWD1194 figure 2

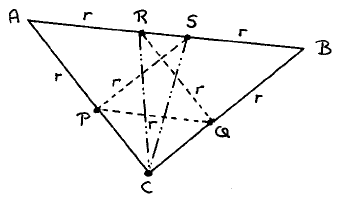
conclude that, with AP = r and BQ = r, we have PQ = r. Completing the diamonds with AR = r and BS = r, we conclude RQ = r and PS = r. Being the hypotenuse of a right-angled triangle with side = r, RC and SC are both > r.

In the case that neither A nor B belongs to a desired pair, A and B —more than r apart— are of different colour, and P, S, C, R, Q —all ≥ r apart from A and B— are all of the remaining 2 colours. Consequently, in the cyclic arrangement P, S, C, R, Q of these 5 points, 5 being odd, two successive points are of the same colour. Their mutual distance being at least r, they form a desired pair. QED.

*         *         *

In the above argument we have appealed to the following theorem:

Consider a finite undirected graph in which each vertex is of degree 2. If each vertex is of one of 2 colours and the number of vertices is odd, there exists an edge that connects a vertex to a vertex of the same colour.

The proof is by double application of the pigeon-hole principle. Let the number of vertices —which equals the number of edges— be 2n+1. Since there are 2 colours, there are at least n+1 vertices of the dominant colour; as they are all of degree 2, they give rise to 2n+2 endpoints of the dominant colour. Since there are “only” 2n+1 edges, at least 1 of them has 2 endpoints of the dominant colour.

Austin, 25 December 1994

prof.dr. Edsger W.Dijkstra
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712-1188
USA