Dana Moshkovitz: An Overview of My PhD

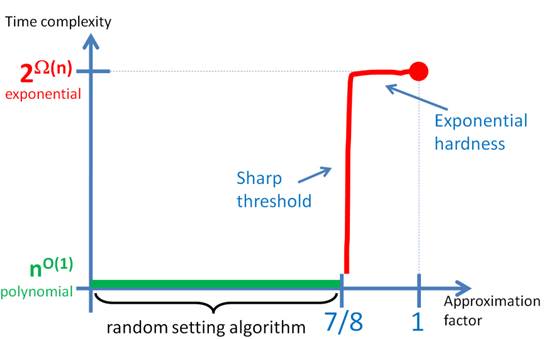
My PhD

Ran Raz and I showed that approximating Max-3SAT and other problems exhibit a sharp phase-transition in their computational hardness.

That is, if you assume (exact) 3SAT takes exponential-time 2^W(n), and you plot the approximation factor on one axis,

and the time complexity of achieving this approximation on the other axis, then the graph for approximating Max-3SAT looks like this:

In other words, obtaining any approximation better than 7/8+o(1) takes (nearly-)exponential time, while obtaining (7/8)-approximation is polynomial (in fact, linear) time, due to a simple random setting algorithm.

The drop from exponential time to polynomial time is sharp: it occurs at a window of width o(1) at 7/8.

By the work of Håstad in 1997, it was known that any approximation better than 7/8+e of Max-3SAT for a constant e>0 is NP-hard, and the lower bound on the time complexity was 2^{n^{f(e)}} for some fixed increasing function f of e.

This left open the possibility that the computational threshold at 7/8 is coarse. In particular, it was open whether a sub-exponential time algorithm could be given for sufficiently loose constant approximation e<1/8.

Our work eliminated these possibilities, and showed that the computational phase transition is sharp.

Our work is applicable not just for Max-3SAT, but for all of Håstad’s problems, and for many other problems. The reason for the wide-applicability is that we proved the type of PCP Theorem (known as Label-Cover or projection games) one typically bases optimal hardness of approximation on, and our PCP Theorem had record parameters: soundness error 1/(logn)^b for some b>0 (the important thing is that the error goes to zero with n) and almost-linear length.

What gets into the proof? For the few years before we obtained this result, we developed techniques for randomness-efficiency in algebraic PCPs. These techniques ended up being useful, enabling almost-linear length, but it wasn’t until we had a new technique for composition that we managed to get the PCP in the form crucial to hardness of approximation (Label-Cover/projection games).

The main algebraic problem we considered was low degree testing:

Fix a finite field F and natural numbers m and d, as well as a function f:F^m -> F. If f is a polynomial of degree at most d, then f’s restriction to every line in F^m is a univariate polynomial of degree at most d.

The converse is also true – if the restriction of f to every line is a univariate polynomial of degree at most d, then f is an m-variate polynomial of degree at most d.

The low degree testing theorem says that if the restriction of f to a small fraction of the lines is somewhat close to a univariate polynomial of degree at most d (i.e., there exists a univariate polynomial of degree at most d that agrees with f on a small fraction of the points in the line), then f must be close to an m-variate polynomial of degree at most d.

Rubinfeld-Sudan initiated this study in the 1990’s, and the theorem was proven by Arora-Sudan, 1997 (a similar theorem was proven at around the same time by Raz-Safra). It is the main theorem that goes into the construction of algebraic PCPs.

In this paper we devised a small collection of constant-dimensional subspaces, of size |F^m|^1+o(1) (as opposed to the quadratic size ~|F^m|² of the family of all lines in F^m) such that the theorem still holds.

In this paper we showed how to use this theorem to derive randomness efficient PCPs.

Finally, in this paper we developed the new composition technique which allowed us to prove a projection PCP theorem with low error.