|
|
|
Fast Contour Matching Using
Approximate Earth Mover's Distance |
|
|
|
Kristen Grauman and Trevor Darrell |
|
|
||||||||||||
|
Abstract Weighted graph matching is a good way to
align a pair of shapes represented by a set of descriptive local features;
the set of correspondences produced by the minimum cost matching between two shapes'
features often reveals how similar the shapes are. However, due to the
complexity of computing the exact minimum cost matching, previous algorithms
could only run efficiently when using a limited number of features per shape,
and could not scale to perform retrievals from large databases. We
present a contour matching algorithm that quickly computes the minimum weight
matching between sets of descriptive local features using a recently
introduced low-distortion embedding of the Earth Mover's Distance (EMD) into
a normed space. Given a novel embedded
contour, the nearest neighbors in a database of embedded contours are
retrieved in sublinear time via approximate nearest
neighbors search with Locality-Sensitive Hashing (LSH). We demonstrate
our shape matching method on a database of 136,500 images of human
figures. Our method achieves a speedup of four orders of magnitude over
the exact method, at the cost of only a 4% reduction in accuracy. CVPR04 paper on this work: pdf
Unfortunately, computing the optimal
matching for a single shape comparison has a complexity that is superpolynomial in the number of features. The
complexity is of course magnified when one wishes to search for similar
shapes (``neighbors'') in a large database: a linear scan of the database
would require computing a comparison of superpolynomial
complexity for each database member against the query shape.
Hierarchical search methods, pruning, or the triangle inequality may be
employed, yet query times are still linear in the worst case, and individual
comparisons maintain their high complexity regardless. To address the computational complexity of
current correspondence-based shape matching algorithms, we propose a contour
matching algorithm that incorporates these approximation techniques and
enables fast shape-based similarity retrieval from large databases. We
embed the minimum weight matching of contour features into L1 via
the EMD embedding of [Indyk & Thaper 2003], and then employ sublinear
time approximate NN search to retrieve the shapes that are most similar to a
novel query. The embedding step alone reduces the complexity of
computing a low-cost correspondence field between two shapes from superpolynomial in the number of features to O(nd log(V))),
where n is the number of features, d is their dimension, and V
is the diameter of the feature space. In this work we also introduce the idea of
a low-dimensional rich shape descriptor manifold. Using many examples
of high-dimensional local features taken from shapes in an image database, we
construct a subspace that captures much of the descriptive power of the rich
features, yet allows us to represent them compactly. We build such a
subspace over the ``shape context'' feature of [Belongie
et al 2002], which consists of local histograms of edge points, and
successfully use it within the proposed approximate EMD shape matching
method.
We have demonstrated our fast contour
matching method on datasets of 136,500 human figure images (real and
synthetic examples). We report on the relative complexities (query time
and space requirements) of approximate versus exact EMD for shape
matching. In addition, we study empirically how much retrieval quality
for our approximate method differs from its exact-solution counterpart
(optimal graph matching); matching quality is quantified based on performance
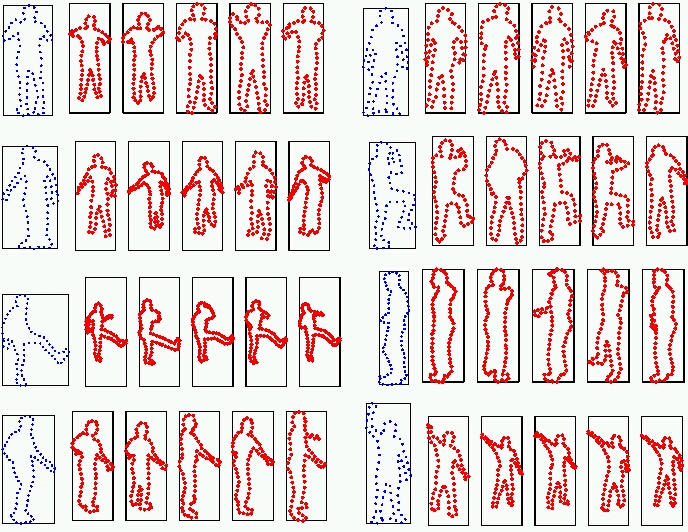
as a k-NN classifier for 3-D pose. Below are
some example database retrievals found with our contour matching
method. Please see this paper for more details on
this work and experimental results: pdf
|
||||||||||||