Action: CheckOut(b,t) "Check out book b from the library at time t" Preconditions: Now(t), TimeAfter(t,n), LibraryOpen(t) Add: HaveBook(b), Now(n) Delete: Now(t) Action: Read(b, t) "Read book b at time t" Preconditions: HaveBook(b), Now(t), TimeAfter(t,n), HomeworkDone(c) Add: BookRead(b), Now(n) Delete: Now(t) Action: DoHomework(c,t) "Do homework for class c at time t" Preconditions: Now(t), TimeAfter(t,n), Assigned(c) Add: HomeworkDone(c), Now(n) Delete: Now(t)
Where the state predicates are interpretted as follows:
Now(t) "The time is now t" TimeAfter(t,n) "The next time after t is n" LibraryOpen(t) "The library is open at time t" HaveBook(b) "You have book b" Assigned(c) "Homework was assigned for class c" HomeworkDone(c) "Homework for class c is done" BookRead(b) "Book b was read"
Consider the initial state:
Now(7:30PM)
TimeAfter(7:30PM, 8:30PM)
TimeAfter(8:30PM, 9:30PM)
TimeAfter(9:30PM, 10:30PM)
LibraryOpen(7:30PM)
Assigned("CS343")
And the conjunctive goal (given in this order):
BookRead("One Hundred Years of Solitude") & HomeworkDone("CS343")
a) Show a detailed, nested trace of subgoals and actions (like that given on pages 19-22 of the lecture notes on planning) resulting when STRIPS is used to solve this problem. Assume that different instantiations of an action (i.e. different ways of binding its variables) that are capable of achieving a goal (such as different times of preforming an action) are considered as alternative actions for achieving the goal. Assume that when there are multiple action instantiations for achieving a goal, that STRIPS first considers the action instantiation with the least number of currently unsatisfied preconditions. Finally, clearly show the final plan constructed and all the facts that are true in each state of the world after each action is executed.
b) Would STRIPS be able to solve this problem if the order of the goals
were reversed? Would it get an optimal solution, a suboptimal solution, or no
solution at all? Briefly explain exactly what would happen in this case.
- ``prototype for an object in Object-Oriented Programming(OOP)'';
- ``education imparted in a series of lessons or class meetings'';
- ``people having the same social or economic status'';
- ``people'' (``People often forget to define a deconstructor for their class'', ``People are often late to class'', ''The struggle of lower class people is the driving force of progress'');
- ``program'' (``This program does not use the window class'', ``This class is a required part of the natural science program'', ``The government's tax program does not address the needs of the lower class'');
- ``student'' (``This window class was written by a clever student'', ``The student was late to class'', ``The student was concerned with the problems of the working class'');
- ``education'' (``Learning how to write an abstract class is a vital part of your education'', ``Not attending the class will hamper your education'', ``Lowering the cost of education is an important issue for the middle class'').
| m | OOP | lessons | economic status | |
|---|---|---|---|---|
| P(m) | 0.1 | 0.6 | 0.3 | |
| P(`people' | m) | 0.001 | 0.1 | 0.1 | |
| P(`program' | m) | 0.1 | 0.01 | 0.001 | |
| P(`student' | m) | 0.01 | 0.2 | 0.01 | |
| P(`education' | m) | 0.005 | 0.05 | 0.05 |
Consider using a naive Bayesian framework in which we assume the probability of
each evidence word is independent given the meaning of the target ambiguous
word. Assume the generative model illustrated on slide 15 of the packet on
"Probabilistic Reasoning and Naive Bayes," where each word is treated as a
binary feature (not the text categorization model illustrated in slide
29). Compute the posterior probability for each of the possible
meanings of ``class'' for the following case:
P(m | not `people',
`program', `student', not `education') (e.g. ``Did the student complete the
homework program for the class?'')
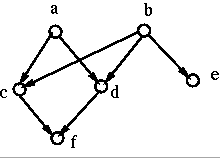
a) What is the minimal number of conditional-probability parameters needed to fully specify this network?
b) What is the minimal number of conditional-probability parameters needed to specify the complete joint probability distribution for this problem?
c) Consider the following interpretation of the network: a is smoking, b is having a cold, c is sore throat, d is inflammed lungs, e is sneezing, and f is coughing. Assume that parameters are set to reasonable values to model this problem, i.e. that a and b both tend to cause both c and d to be true and that b also tends to cause e to be true. Assume we first learn that coughing is true and we compute that smoking is the most likely explanation. Next we learn that sneezing is true. Qualitatively, what happens to the probability of smoking, does it go up or down? According to the theory of Bayes nets, why does this happen?
P(shop) = 0.25
P(rob) = 0.02
P(enter-store | !shop, !rob) = 0.01
P(enter-store | shop, !rob) = 0.80
P(enter-store | !shop, rob) = 0.50
P(enter-store | shop, rob) = 0.90
P(point-gun | rob) = 0.70
P(point-gun | !rob) = 0.01
a) Assuming that the above conditional probabilities are sufficient to specify the CPTs for a Bayes net for this problem, draw a picture for such a Bayesian network.
b) Compute the full joint probability table for this Bayesian network.
Please model your table after the following template:
| shop | !shop | ||||
| rob | !rob | rob | !rob | ||
| enter-store | point-gun | ||||
| !point-gun | |||||
| !enter-store | point-gun | ||||
| !point-gun | |||||
Calculate (show your work):
c) P(enter-store)
d) P(shop | enter-store)
e) P(rob | enter-store)
f) P(shop | enter-store, point-gun)
g) P(rob | enter-store, point-gun)