CS 314 Assignment 2: Recursion and Lists

Due: September 21, 2017 via Canvas.

Files: Cons.java test2.lsp

This assignment may be done in Java or in Lisp.

Write a recursive function sumsq(int n) that adds up the squares of the integers from 1 through n.
Giuseppe Peano (1858 - 1932) showed that all arithmetic operations on natural numbers (nonnegative integers) could be reduced to a single constant (0) and an operation successor, which is available in Java as ++ (in Lisp, 1+).
Write a recursive function peanoplus(int x, int y), using only ++ and --, to perform addition according to the following definition:
peanoplus(x, y) = x, if y = 0; peanoplus(x + 1, y - 1), otherwise.
Note that the ++ and -- operators must appear before the operands in the recursive call, so that the change will be made before the call; otherwise, the change will be made after the call, causing an infinite loop.
We can think of peanoplus as similar to an algorithm for adding together buckets of rocks: if the second bucket is empty, stop; otherwise move one rock from the second bucket to the first bucket and continue.
Can you think of an invariant (property that is always true) of peanoplus? What is the Big O of peanoplus? This function is naturally tail-recursive.
Write a function peanotimes(int x, int y) that multiplies two integers using only peanoplus, ++, and --, and is written in a recursive style similar to that of peanoplus. What is the Big O of peanotimes?
The mathematical notation , read n choose k, is used to denote the number of distinct subsets of k items that can be chosen from a set of n distinct objects. It can be shown that:

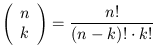
Although the factorial function could be used in implementing n choose k, this would be inefficient for large values of n and small k. We have also seen that factorial quickly overflows the available accuracy of the basic types in Java. n choose k has the value 1 when k = 0. We can algebraically rewrite the definition into the following form for k > 0:

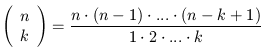
Write a function choose(int n, int k), using a tail-recursive auxiliary function, to compute n choose k without using the factorial function. Note that the above equation has k terms in both the numerator and the denominator; multiply by the numerator term before dividing by the denominator term to ensure that the numerator is evenly divisible by the denominator term.
Write functions sumlist(Cons lst) to add up a list of Integer. Iterative versions sumlist and sumlistb are given. Write other versions of this function: sumlistr (recursive), and sumlisttr (tail-recursive using an auxiliary function).
Write a function sumsqdiff(Cons lsta, Cons lstb) to sum squared item-by-item differences Σ(x_i - y_i)² of two lists of Integer. Write several versions of this function: iterative, recursive, and tail-recursive using an auxiliary function.
Write a function maxlist(Cons lst) to find the maximum value in a list of Integer. Write several versions of this function: iterative, recursive, and tail-recursive using an auxiliary function.
Binomial coefficients are the numeric factors of the products in a power of a binomial such as (x + y)ⁿ. For example, (x + y)² = x² + 2 x y + y² has the coefficients 1 2 1. Binomial coefficients can be calculated using Pascal's triangle:
```
            1                   n = 0
         1     1
      1     2     1
   1     3     3     1
1     4     6     4     1       n = 4
```
Each new level of the triangle has 1's on the ends; the interior numbers are the sums of the two numbers above them. Write a program binomial(int n) to produce a list of binomial coefficients for the power n using the Pascal's triangle technique. For example, binomial(2) = (1 2 1). You may write additional auxiliary functions as needed. binomial should be a recursive program that manipulates lists; it should not use (choose n k). Use the function (choose n k) that you wrote earlier to calculate (choose 4 k) for k from 0 through 4; what is the relationship between these values and the binomial coefficients?