With M discrete memory storage slots, the problem then arises as to how
a specific training example should be generalized. Training examples are
represented here as 
, consisting of an angle 
,
an action a, and a result r where 
is the initial position
of the defender, a is ``s'' or ``p'' for ``shoot'' or ``pass,'' and
r is ``1'' or ``-1'' for ``goal'' or `` miss'' respectively. For
instance, 
represents a pass resulting in a goal for
which the defender started at position 
on its circle.
The most straightforward technique would be to store the result at the
single memory slot whose index is closest to 
, i.e., round
to the nearest 
for which Mem[ 
] is
defined, and then set 
. However, this technique does
not provide for the case in which we have two training examples
and 
, where 
and 
both round to the same 
. In particular, there is no way of
scaling how indicative 
is of 
.
In order to combat this problem, we scale the value stored to
by the inverse of the distance between 
and
relative to the distance between memory indices. A result
r at a given 
is multiplied by 
before being stored to Mem[ 
]. In this
way, training examples with 
's that are closer to 
can
affect Mem[ 
] more strongly. For example, with M = 18 (so
Mem[ 
] is defined for 
), 
causes
to be updated by a value of 
. Call this our basic memory storage
technique:
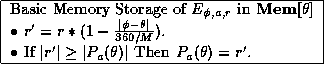
Using this generalization function, the ``update'' of 
would
only have an effect at all if 
prior to this
training example. Consequently, only the past training example for
action a with 
closest to 
is reflected in
: presumably, this training example is most likely to
accurately predict 
. Notice that this basic memory
storage technique is appropriate when the defender's motion is
deterministic. In order to handle variations in the defender's speed,
we introduce later a more complex memory storage technique. The
method of scaling a result based on the difference between 
and
will remain unchanged.
In our example above, 
would not only
affect Mem[120]: as long as 
was not already larger,
its value would be set to 
.
Notice that any training example 
with 
could override this value. Since 116.5 is so much closer
to 120 than it is to 100, it makes sense that 
affects
Mem[120] more strongly than it affects Mem[100]. However,
would affect both memory values equally. This memory
storage technique is similar to the kNN and kernel regression function
approximation techniques which estimate 
based on 
possibly scaled by the distance from 
to 
for the k
nearest values of 
. In our linear continuum of defender
position, our memory generalizes training examples to the 2 nearest
memory locations.