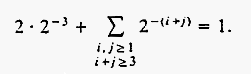EWD 1200

Only a matter of style?

For educational purposes we analyse the opening pages of an 11-page article that appeared in The American Mathematical Monthly, Volume 102 Number 2 / February 1995. We added line numbers in the right margin.

line 4: Since in this article, squares don’t get alternating colours, it could be argued that the term “chessboard” is misplaced.

line 4: The introduction of the name “B” seems unnecessary: it is used —in the combination “the board B”— in the text for Figure 1 and in line 71; in both cases just “the board” would have done fine. In line 77 occurs the last use of B, viz. in “X ⊂ B”, which is dubious since B was a board and not a set; in line 77, I would have preferred “Given a set X of cells”.

line 7/8: The first move, being a move like any other, does not deserve a separate description. The term “step” is redundant.

line 8: Why not “a move consists of”?

line 10/11: At this stage the italics are puzzling, since a move is possible if, for some i, j, cell (i, j) contains a pebble and cells (i+1, j) and (i, j+1) are empty.

line 10: Twice the term “positions” for what everywhere else is called “cells”.

line 12: Why not “After k moves the board had k+1 pebbles on it”?

line 12/14: In the one sentence, k counts moves, in the other k counts pebbles. Since the prose does not indicate the scope of dummies, this double use of the same k is a little bit unforgivable.

line 14: “and we set R := ∪k≥1 R(k)”. We remark
•   the use of the verb “to set” when defining (the set!) R can be considered unfortunate
•   since “R” is not used on the next two pages, the name seems to be introduced too early
•   the introduction of the name R seems unnecessary; in the rest of the paper I saw it used once in “any C ∈ R”, where “any reachable configuration” would have done. (Note. In the context in question —p 116— the reachable context can remain anonymous: the quoted occurrence of C is the only occurrence of the identifier C in that context. My conclusion is that the reachable configuration has been called C only in order to admit the boolean expression C ∈ R.)
•   the authors have chosen a special symbol for what is sometimes referred to as “definitional equality”; they are not the only ones to do so, but I would like to remark that I have never seen a proper justification of the convention (nor can I think of one)
•   after the introduction of ALGOL60, the mathematical community has adopted the latter’s assignment operator as symbol for “definitional equality”, thereby only adding to the confusion since assignment has nothing to do with equality (vide x:=x+1)
•   identifier R has been given two meanings, in particular the type of R is no longer defined: the one R is of the type “set of cells”, the other R is of type “natural number” → “set of cells”.

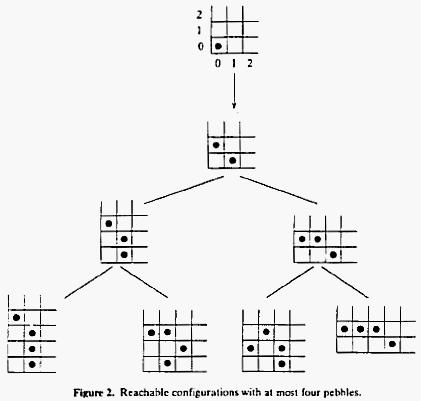
line 15: Why not “the eight reachable configurations”? The printed text raises the question of how a reachable configuration can be impossible.

line 17: The printed text refers to an obligation for pebbles; had it been “some cell having coordinates (i, j) with i+j ≤ 3 must contain a pebble”, we would have had an obligation for cells! It is better to avoid this spurious dilemma by deleting “must” —a verb that is usually better avoided— and to write “some pebble occupies a cell” or “some cell contains a pebble”.

line 17/18: I think the authors meant “This fact seems to have noted first by M.Kontsevich.”

line 19/22: We remark
•   in a sentence of the structure “If L(k) denotes the set {(i, j): i + j = k} then [.....].” the scope of the convention stated in the antecedent ends at the end of the consequent; in this paper, the scope of L’s definition extends through the whole paper!
•   in line 20, L(1) ∪ L(2) ∪ L(3) should be L(0) ∪ L(1) ∪ L(2) ∪ L(3); L(0) is also missing in Lemma 2.
•   in line 21, delete “must always”: “any reachable configuration has a pebble...”. [Now I come to think of it, “some cell” is okay, for the cells are distinguished by their coordinates; “some pebble” is nonsense, for the pebbles are as indistinguishable as the electrons in the helium atom.]

line 38, 45, 47 & 49: add “L(0) ∪”.

line 39: It is a pity that the weight of cell (i, j) has been given as 2−(i+j), instead of as (½)i+j or rather (½)i · (½)j, the latter being a special case of pi·qj with p+q=1. (The latter equality equivales the requirement that a move does not change the total weight covered.) The unproved statement about the boundaries —line 53/55— follows via (p, q)=(1,0) and (p, q)=(0,1)

line 42: I would prefer “the total weight of the cells covered”; as printed, it might be misread as “the weights of cells covered”. I would also prefer “covered” replaced by “occupied”, the term used before.

line 52, 56, 58, 60: add “L(0) ∪”.

line 55: replace “which” by “that”. (That was easy.).

line 55/59: These two sentences have baffled me for at least 15 minutes —and this was when I really got cross with the authors—. Forget about minor problems such as “weight covered” —on top of this page [line 42], cells were the things being covered—; what hit me was “can” in line 55 and “these cells” in line 58. Eventually I realized that the verb “can” hints at a hidden inequality: the conclusion that should have been drawn is that the total weight of the cells outside L(0) ∪ L(1) ∪ L(2) but with only one cell from each of the boundaries is at most 1. From line 58, “must” is again a candidate for deletion. Furthermore, authors should know that an obscure notion like “these cells” is not clarified by printing the preceding “all” in italics.

line 67/71: “It might be helpful”: helpful for what purpose and how? “in this model”: in which model? “the pebbles first move”: what is the meaning of “first”? The text mentions no “later” or “second”; “are identified in the obvious way”: how obvious?

line 74: delete “in fact”, as it does not contribute anything

line 75: the introduction of the adjective “standard”, which is used nowhere else, serves no purpose.

line 72: This sentence has no connection to what precedes it, and is closely connected to what follows it; this is not reflected in the vertical spacing, which obscures the logical structure of the text. Moreover, it would have been nice if “the easy induction argument” had been shown: a few colleagues and I spent 1½ hours on not finding it.

line 75: The introduction of the adjective “standard” as technical term is superfluous, since the term is not used in the rest of the paper.

line 77/81: • This paragraph displays the (not uncommon) shortcoming that its logical relation to the rest of the text requires the study of its contents. Is it going to demonstrate Lemma 3 or is it an introduction to Theorem 1? (At first reading, I assumed the former, and got puzzled.)
•   It is elliptic: line 77 announces the definition of the set M(X), but lines 78 through 81 formally don’t do so (they don’t mention M(X) ).
•   It is very obscure. The notation M(X) strongly suggests that the paragraph should define a function of type: “set of cells” → “set of moves”. The text, however, describes a process that seems to depend on an initial distribution of pebbles. But there is more ambiguity. Suppose there are 2 cells, one in X and one not in X, but both containing pebbles; we are then to remove pebbles either from the one or from the other: how do we choose? Also, how do we “remove all but at most one of the pebbles”? For me, “at most one” is in natural numbers “zero or one”, but the removal of “all but zero or one of the pebbles” is too nondeterministic to define a function. For the dependence on the initial pebble distribution I can suggest a fix, but not for the rest of the ambiguities.

It is here that I gave up. When studying a paper I don’t consider it my duty to conjecture what should have been written down.

*         *         *

The above has been written for my students with the intention of helping them to improve the quality of their writings.

Austin, 22 February 1995

(Followed by EWD1200-8, 9, 10)

prof.dr. Edsger W.Dijkstra
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712-1188
USA

 


[The American Mathematical Monthly, Vol.102 No.2 / February 1995, pages 113-115]

 

Pebbling a Chessboard
Fan Chung, Ron Graham, John Morrison,
and Andrew Odlyzko


1. INTRODUCTION. The following puzzle has attracted some attention recently.
We first learned of it through Martin Gardner [6]. A version of it appeared in
Omni magazine in 1993 [11]. However, it was proposed over 10 years ago by
Kontsevich [9], and a partial analysis of it was published shortly thereafter by
Khodulev [8]. We begin with an infinite “chessboard” B covering the first quad- 		0
rant. The cells of the board are labelled by integer coordinates (i, j) with i, j ≥ 0.
Initially, a single “pebble” is located in cell (0,0) (the lower left corner; see Figure
1). The first step or “move” consists of replacing this pebble by two pebbles,
located at cells (1,0) and (0,1), respectively. In general, a move will consist of
removing some pebble, say in cell (i, j), and replacing two pebbles on the board, in 		5
positions (i + 1, j) and (i, j + 1), provided each of these positions is not already
occupied. 		10
EWD1200 figure 1
 
    After k steps the board will have k + 1 pebbles on it. We call such configura-
tions of pebbles reachable configurations. We will denote by R(k) the set of
reachable configurations with k pebbles, and we set R := ∪k≥1 R(k). In Figure 2,
we show the eight possible reachable configurations with at most four pebbles.
    A little experimentation convinces one that in any reachable configuration,
some pebble must occupy a cell having coordinates (i, j) with i + j ≤ 3. This fact
first seems to have been noted by M. Kontsevich [9]. We give the “book” proof of
this in the next section. If L(k) denotes the set (or “level”) {(i, j): i + j = k} then 		15
EWD1200 figure 2
 
we can express the above assertion by saying that L(1) ∪ L(2) ∪ L(3) is unavoid-
able, i.e. any reachable configuration must always have some pebble in a cell in
L(1) ∪ L(2) ∪ L(3). In general, an unavoidable set is one which intersects every
reachable configuration. Of course if  S  is unavoidable and  T ⊇ S  then  T  is
unavoidable. Let us call S a minimal unavoidable set if S is unavoidable but no 		20
proper subset of S is, and let M(k) denote the family of minimal unavoidable sets
with k cells.
    In this note we will characterize the elements of M(k) and give a polynomial
time algorithm for recognizing such elements. Many of these results were first
proved by Khodulev [9], and we present them here for completeness, since the 		25
paper [8] is not widely available and contains only sketches of proofs. We will also
determine the asymptotic growth rates of r(k) := |R(k)| and m(k) := |M(k)|, the
sizes of R(k) and M(k), respectively, as k → ∞. (These results are all new.) It
turns out that the analysis of r(k) and m(k) leads to some interesting problems in
asymptotic enumeration. 		30
    Further results on this problem, including generalizations to arbitrary partially
ordered sets, have been obtained by Eriksson [4].

2. PROPERTIES OF UNAVOIDABLE SETS

Lemma 1. [9] The set L(1) ∪ L(2) ∪ L(3) of all (i, j) with i + j ≤ 3 is unavoidable.
Proof: To each cell (i, j) assign the weight 2−(i+j). Observe that: 		35
(i)  The total weight covered by pebbles in any reachable configuration is 1.
This is so since the starting cell (0,) has weight 1, and a move does not
change the weight of cells covered, i.e.,
2−(i+j) = 2−((i+1)+j) + 2−(i+(j+1)).
(ii)  The total weight of all cells in the board is ∑i, j ≥ 0 2−(i+j) = 4.
40
(iii)  The total weight of L(1) ∪ L(2) ∪ L(3) is 13/4. Thus, the weight of the
complement of L(3) is only 3/4, and since that is less than 1, cannot
contain all the pebbles of a reachable configuration. Thus L(1) ∪ L(2) ∪
L(3) is unavoidable.∎
    However, L(1) ∪ L(2) ∪ L(3) is not a minimal unavoidable set. The following 		45
result was proved by Khodulev [8]. It was independently conjectured by Martin
Gardner [6]. The proof given here is due to Harold Reiter [14].

Lemma 2. L(1) ∪ L(2) is unavoidable.

Proof: As before, assign the weight 2−(i+j) to the cell (i, j). Observe now that any
reachable configuration  C  has exactly one pebble on each of the boundaries
 50
{(i,0): i ≥ 0} and {(0, j): j ≥ 0}. Thus, the total weight which C can cover outside
of L(1) ∪ L(2) is
 55
EWD1200 figure 3
 
This implies that if C is to avoid L(1) ∪ L(2), it must cover all these cells, which is
impossible since C is finite.∎    
    However, L(1) ∪ L(2) is not minimal either, as we will see later.
    We should observe that for any reachable configuration C, the set of moves
needed for reaching C is unique. Only the order in which these moves are
executed can vary in the different ways of reaching C.
    Suppose now that we relax the rules for moves by allowing the replacement of a 		60
pebble at (i, j) by pebbles at (i + 1, j) and (i, j + 1) even when these positions
might already be occupied by pebbles. In other words, we allow the accumulation
of multiple pebbles in cells during the process of reaching C. It might be helpful
for this model to imagine that the pebbles first move onto the vertices of an
infinite binary tree rooted at (0,0). Then the 2k vertices in the kth level of the 		65
tree are identified in the obvious way with the k + 1 cells in the kth level L(k) :=
{(i,j): i + j = k} of the board B.
    An easy induction argument now establishes the following result

Lemma 3. If a configuration of pebbles (with at most one pebble per cell) can be
reached by moves which allow accumulations of pebbles in cells, then in fact it can 		70
also be reached by the “standard” moves, i.e., those which do not allow accumu-
lation.

    Given a set X ⊂ B, we define the set M(X) of moves recursively as follows.
Starting at level 0 and proceeding one level at a time by increasing levels, perform
the moves required either to remove all pebbles from a cell in X, or to remove all 		75
but at most one of the pebbles from a cell not in X. Continue through the last
level L(h(X)) containing a cell of X.

Theorem 1. X ⊂ B is unavoidable if and only if after executing the moves in M(X),
some cell contains at least 3 pebbles.
 80


(End of EWD1200)