Public Key Cryptography: RSA

There are many kinds of cryptosystems, or schemes for encoding and decoding information in this way. For example, a substitution cipher where you use one letter to stand for a different one, e.g., 'A' might stand for 'F', and 'P' for 'Y', etc. You have probably seen this scheme presented as a puzzle in your Sunday newspaper; they are easy to break.

A more secure system is the RSA public-key cryptosystem. A public-key cryptosystem is one in which anyone who participates has two keys; these are like a password for encrypting and decrypting data. You have a public key and a private key. When someone wants to send you a message, they use your public key (which you have published somewhere) to encrypt the data. They send you the encrypted message which you decrypt with your private key, which you keep secret. The public key is only good for encrypting, not decrypting, so communication is secure.

The RSA system is based on the difficulty of finding the prime factors of large numbers versus the relative ease of finding out whether a large number is prime. Generating the keys for RSA is a matter of testing for primality. Encoding a message is a matter of doing something knowing a large integer, without knowing the factors. Decoding a message is dependant on knowing the factors. For 300 or more digit numbers, finding the prime factors is impossible in a reasonable amount of time with today's best algorithms, and is likely to remain so in the future.

This is how the RSA system works. A participant creates his public and private keys like this:

1. Select at random two large prime numbers p and q. They might be around 150 digits each.
2. Let n = pq.
3. Select a small odd integer e that is relatively prime to (n). is the totient function giving the order of the multiplicative group mod n; in the case of the product of two primes, this number if (p-1)(q-1).
4. Let d be the multiplicative inverse of e, mod (n). This means we find an integer d such that de (mod (n)) = 1. An efficient algorithm exists for computing d from e.
5. Publish P = (e,n) as the public key.
6. Keep S = (d,n) secret as the private key. Messages are represented by large integers. Since data in a computer is really just a sequence of bits, we can think of these bits collectively as a big number. We break up the message into blocks such that each block is a number less than n.

   To encrypt a message block M with the public key P = (e,n), we take M^e (mod n).

   To decrypt a ciphertext (i.e. encrypted block) C, using the private key S = (d,n) we apply the reverse operation, taking C^d (mod n).

   Modular Arithmetic

   When we say "do something mod n," it means that the result of the arithmetic operation should be taken modulo n, i.e., we take the remainder when dividing by n. For instance, 7 times 6 (mod 5) is 2, since 42 mod 5 is 2. The multiplicative inverse of a number e mod n is a number d such that ed (mod n) is 1. For example, 3 is the multiplicative inverse of 7 (mod 5), since 3 * 7 (mod 5) = 1.

   There is a rich theory of modular arithmetic and number theory in general upon which RSA is based. We won't go into the complex issues involved there, rather, we'll see some of the algorithms that go into implementing RSA and some of the algorithms that try to break it.

   Modular Exponentiation

   RSA requires us at certain points to raise a large number to a large power mod n. We will assume, when appropriate, that we have some sort of relatively efficient implementation of large number arithmetic of the kind discusses in the last lecture. Let's look at a first try at modular exponentiation:

   // returns ab (mod n)
   Mod-Exp-1 (a, b, n)
   	product = 1
   	for i in 1..b do
   		product = product * a
   	end for
   	return product % n
   

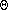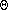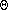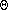   Let's analyze this algorithm. It does (b) multiplications. Recall that in RSA, a could be a 300 digit number. The number of digits required to store a number a is (log a); the number of digits required to store a^b is thus (log a^b), = (blog a). If b is also very large (as it could be in the case of decryption), we will require huge amounts of storage just to store that quantity. So if a and b are both 300 digit numbers, we will need around 300 * 10³⁰⁰ = 3 * 10³⁰² digits to store product. This is substantially more than the number of elementary particles in the known universe, so it is unlikely to be successfully allocated by malloc().

   An improvement that doesn't require such astronomical storage is to do the modulus operation each time through the loop, so that we can keep product small:

   // returns ab (mod n)
   Mod-Exp-2 (a, b, n)
   	product = 1
   	for i in 1..b do
   		product = product * a
   		product = product % n
   	end for
   	return product
   

   Now, the size of product can never exceed twice the size of a, so we may require up to 600 digits of storage. However, if b is still large, e.g., 300 digits, then the loop will have to iterate about 10³⁰⁰ times. Assuming a (very generous) time of one nanosecond per loop iteration, this would take about 3.16 times 10²⁸⁰ years to complete. It is conjectured that the universe itself is only about 2 times 10¹³ years old, and will experience heat death due to the second law of thermodynamics long before 10²⁸⁰ years from now, so this is also an unacceptable algorithm.

   Suppose you want to find 2⁸. You could multiply 2 by itself 8 times, 2*2*2*2*2*2*2*2 = 256, or simply square repeatedly log₂ 8 = 3 times, getting 2²=4, 4² = 16, 16² = 256. This method only works for exponents that are powers of 2 like 8, but there is an easy generalization that allows us to use any exponent. This yields the following algorithm for modular exponentiation:

   // returns ab (mod n)
   Mod-Exp (a, b, n)
   	product = 1
   	y = a
   	while b > 0 do
   		if b is odd then 
   			product = (product * y) % n;
   		endif
   		y = (y * y) % n;
   		b = b / 2
   	end while
   	return product
   

   Let's try this on a small example, first without worrying about the modular part: Let a=2, b=10.

   	product b       y
   init	1       10      2
   	1       5       4
   	4       2       16
   	4       1       256
   	1024    0       65536
   

   y keeps track of the "current" power of 2, which we keep squaring through the loop. If b is odd, then at that point in the binary representation of b, there is a 1 bit; this means there is an extra factor of a that wouldn't appear if b were a perfect power of two, so we multiply it in.

   The analysis is much less grim. Since we are dividing b by 2 each time, the loop can only go log₂ b times before b=0. Each multiplication and modulus takes the square of the number of digits involved, which is bound above by log n. So the whole loop takes time O(log b log²n). For 300 digit numbers, this takes a few seconds or less on an average computer.

   Testing for Primality

   In RSA, we need a way to generate large primes. One way to do this is to generate a large odd random number (by e.g. having the user bang on the keyboard and use the input as a seed to a random number generator), then test the number for primality. If it can be proved not to be prime (i.e., it is composite), then we try that number plus 2 (i.e. excluding even numbers), plus 4, 6, etc. until we find a prime number. The Prime Number theorem assures us that we will find a prime number within a distance proportional to the logarithm of the first number, i.e., relatively quickly.

   How do we determine whether a number p that we suspect is prime is actually prime? There is a theorem in number theory called Fermat's Little Theorem (not to be confused with his famous "Last Theorem" that was proved only recently): If p is prime, then

   a^p-1 = 1 (mod p) for all positive integers a < p.

   For some bases a, you will find some composite numbers n that also satisfy a^n-1 = 1 (mod n); however, the probability that it will be true for one value of a is independent from whether it will be true for a different value of a. Thus, the more values of a we choose and use to verify a^p-1 = 1 (mod p), the more sure we are that p is in fact prime. This assuredness (i.e., the probability that p is prime) doubles for each a we try, and is very high to begin with, so with just a few values of a we can be almost certain that p is a prime suitable for use with RSA. If it isn't, we'll find out quickly enough when the algorithm fails (but this never happens, because we can make the probability that p is not prime arbitrarily low).

   So this algorithm will return False if its parameter is composite and True if the parameter is "probably" prime:

   Probably-Prime (p)
   	for a in 2..20 do
   		if ap-1 != 1 (mod p) return False
   	end for
   	return True
   

   We can simply use the same modular exponentiation algorithm from above to obtain an efficient algorithm.

   Integer Factorization

   The problem of finding the prime factors of a composite numbers is the key component to breaking RSA. This problem is very difficult; the best algorithms know today require superpolynomial (but subexponential) time (when the time is expressed in terms of the number of digits or bits in the number to be factored).

   A simple algorithm is trial division: to factor n, try dividing it by every number from 2..sqrt(n); if there is ever a zero remainder, then you have found a factor. If k is the number of digits in n (i.e., about log₁₀ n), then this algorithm takes O(10^n/2) divisions. For a 300 digit number, this is about 10¹⁵⁰, another one of those astronomical numbers.

   There are other algorithms that perform much better. The Number Field Sieve is arguably the best known algorithm. It runs in time O(exp(sqrt(log k log log k))), which is much better than O(10^k/2), but still superpolynomial. It recently took a distributed effort of thousands of computers running a highly tweaked implementation of this algorithm almost a whole year to find the prime factors of one 129-digit number that was proposed as a challenge in the late 1970s by the authors of RSA. A 300-digit number is totally impossible by today's standards, and those of the forseeable future, barring some breakthrough in algorithms or hardware.