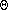 (nk). This is true even if the lower order terms are multiplied by something
in o(n), such as log n (Is this true if we replace o with O?).
(nk). This is true even if the lower order terms are multiplied by something
in o(n), such as log n (Is this true if we replace o with O?).
- a0 = 1
- a- n = 1/an
- (an)m = amn
- anam = an+m
 )n)
for any positive
)n)
for any positive  . Your book has
a nice proof of this using limits.
. Your book has
a nice proof of this using limits.
Some logarithms are use more frequently:
- logex, or natural logarithm. This is usually written as ln x. e is one of those transcendental numbers like pi that come up frequently in mathematics; natural logarithm is often easier to work with so is often preferred.
- log2x. The logarithm base two comes up often in divide-and-conquer algorithms and other areas of computer science. For example, the number of bits required to store a number n in binary is log2n.
- log10x. Log base ten of a number is one less than the number of decimal digits in that number. It gives you an idea of the order of magnitude of a number. Basically, it only comes up because we are used to using a decimal (base 10) number system.
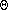 (ln n).
(ln n).