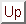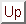

The internal state of the neurons is denoted by 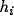 , where
, where
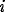 is a two-dimensional Cartesian coordinate for the location of
the neuron. The neurons are arranged on a regular square lattice with
spacing 1, i.e.,
is a two-dimensional Cartesian coordinate for the location of
the neuron. The neurons are arranged on a regular square lattice with
spacing 1, i.e., 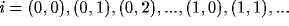 . The
neural activity (which can be interpreted as a mean firing rate) is
determined by the squashing function
. The
neural activity (which can be interpreted as a mean firing rate) is
determined by the squashing function 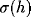 of the neuron's
internal state
of the neuron's
internal state 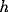 . The neurons are connected excitatorily through
the Gaussian interaction kernel g. The strength of global
inhibition is controlled by
. The neurons are connected excitatorily through
the Gaussian interaction kernel g. The strength of global
inhibition is controlled by 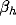 . It is obvious that a blob can
only arise if
. It is obvious that a blob can
only arise if 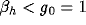 (imagine only one neuron is
active), and that the blob is larger for smaller
(imagine only one neuron is
active), and that the blob is larger for smaller 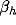 . Infinite
growth of
. Infinite
growth of 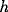 is prevented by the decay term
is prevented by the decay term 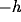 , because it is
linear, while the blob formation terms saturate due to the squashing
function
, because it is
linear, while the blob formation terms saturate due to the squashing
function 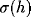 .
The special shape of
.
The special shape of 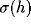 is motivated by three factors.
Firstly,
is motivated by three factors.
Firstly,  vanishes for negative values to suppress oscillations
in the simulations by preventing undershooting. Secondly, the high
slope for small arguments stabilizes small blobs and makes blob
formation from low noise easier, because for small values of
vanishes for negative values to suppress oscillations
in the simulations by preventing undershooting. Secondly, the high
slope for small arguments stabilizes small blobs and makes blob
formation from low noise easier, because for small values of 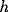 the interaction terms dominate over the decay term. Thirdly, the
finite slope region between low and high argument values allows the
system to distinguish between the inner and outer parts of the blobs
by making neurons in the center of a blob more active than at its
periphery.
Additional multiplicative parameters of the decay or cooperation
terms would only change time and activity scale, respectively, and do
not generate qualitatively new behavior. In this sense the parameter
set is complete and minimal.
the interaction terms dominate over the decay term. Thirdly, the
finite slope region between low and high argument values allows the
system to distinguish between the inner and outer parts of the blobs
by making neurons in the center of a blob more active than at its
periphery.
Additional multiplicative parameters of the decay or cooperation
terms would only change time and activity scale, respectively, and do
not generate qualitatively new behavior. In this sense the parameter
set is complete and minimal.