On a theorem by Lambek and Moser.
While looking for interesting functions mapping sequences of integers into sequences of integers, W.H.J. Feijen found in [1] the following results attributed to J. Lambek and L. Moser.
Let f be an ascending continued concatenation of natural numbers, more precisely:
| (A x : x ≥ 0 : 0 ≤ f x ≤ f (x+1)) , |
| (A F : F ≥ 0 : (E X : X ≥ 0 : (A x : x ≥ X : f x > F))) . |
Let the function C with g = C f be defined by the relation for all y ≥ 0
| g y = (N x : x ≥ 0 : f x ≤ y) |
The first result attributed to Lambek and Moser is that then f = C g, as is illustrated by the example
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ...... | |
| f : | 0 | 1 | 1 | 3 | 6 | 6 | 7 | 8 | 10 | 10 | ...... |
| g : | 1 | 3 | 3 | 4 | 4 | 4 | 6 | 7 | 8 | 8 | ...... |
Let for any continued concatenation q of natural numbers the function D be defined by the relation for all n ≥ 0
| D q n = n + (q n) . |
In the above example we would have
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ...... | |
| D f : | 0 | 2 | 3 | 6 | 10 | 11 | 13 | 15 | 18 | 19 | ...... |
| D g : | 1 | 4 | 5 | 7 | 8 | 9 | 12 | 14 | 16 | 17 | ...... |
The second result attributed to Lambek and Moser is that D f and D g form a partitioning of the natural numbers.
For people willing to generalize pictures the visualization “proves” these results. The elements of f and D f have been
represented by vertical bars, one wide and of the corresponding length, those of g and D g have been represented by a horizontal
ones. The mapping C then becomes a reflection. 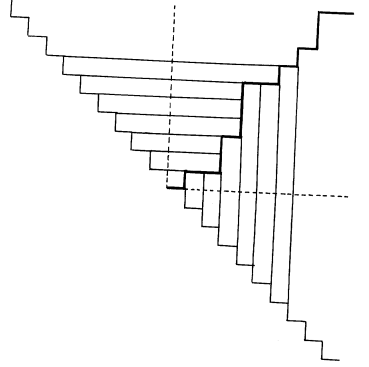
Tracing the plot, we can place the bars in the order of increasing length: bar 14 is next (horizontally), bar 15 vertically, bars 16 and 17 again horizontally, etc.
| [1] | Honsberger, Ross |
| “Ingenuity in Mathematics” | |
| New Mathematical Library, Vol 23 | |
| Mathematical Association of America (1970) |
| Plantaanstraat 5 | 9 October 1980 |
| 5671 AL NUENEN | prof. dr. Edsger W. Dijkstra |
| The Netherlands | Burroughs Research Fellow |
Transcribed by Martin P.M. van der Burgt
Last revision