On a proof I learned from prof. dr. J. Haantjes
In my freshman year at Leyden University (1948-49), dr. J. Haantjes —who, regrettably, died too young— was my only professor that excited and impressed me. He was exciting because he showed types of arguments that were absolutely novel to me, he was impressive because of the calculational agility with which he carried them out.
It was also his first year at the University. In retrospect I think he was as uncertain as to what to expect from his students as we were as to what was expected from us. He spoke softly and wrote small on the blackboard, both rather fast. I think he sinned against almost all educational principles of today, but, fortunately, those did not exist yet. Shy and uncertain, but also brilliant and dedicated, he was revered. He may have had a profound influence on me; if so, that would be for me reason for joy and even some pride.
I vividly remember his proof that the altitudes in a triangle are concurrent —I guess this was November 1948—. Consider the algebraic identity
(0) (a−h) ⋅ (b−c) + (b−h) ⋅ (c−a) + (c−h) ⋅ (a−b) = 0
which depends on symmetry and associativity of addition and multiplication plus the fact that the latter distributes over the former. Since those properties are satisfied by vector addition and the scalar product, (0) also holds if we interpret a, b, c, and h as vectors —from some origin— to points A, B, C, and H respectively. Associating the orthogonality of two vectors with their scalar product being zero, we conclude from (0) that if 2 of the scalar products equal zero, so does the third, hence the altitudes in ∆ABC all go through H. (For convenience’s sake we have confined ourselves to the situation in which A, B, C, and H are all distinct.)
I was absolutely thrilled, remembering only too well the clumsy Euclidean proof on which I had been educated. (Calling the altitudes in the usual fashion AD, BE, and CF, one identifies the altitudes of ∆ABC as the angle bisectors of ∆DEF and then appeals to the concurrency of the angle bisectors of a triangle. This proof is really ugly, since it is very hard to avoid a case analysis on sharp and obtuse triangles; even without that case analysis, it is painfully indirect.) I still remember how thrilled I was.
* *
*
The other night, talking with a good friend about mathematical methodology, I tried to explain the above proof by way of example. In general willing to buy the argument, he yet was unconvinced of its merits because he had not learned how to see at a glance that (0) is valid. In explaining to him how one can see that at a glance, I saw that it would have sufficed to consider
(1) a ⋅ (b−c) + b ⋅ (c−a) + c ⋅ (a−b) = 0
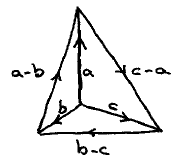
The drawing is simpler —6 vectors instead of 10— and (1) is about twice as easy to verify as (0). I don’t know why Haantjes chose to use (0), for he was a master in the simplest choice of coordinates.
What amazes me most is that, while I have often used this proof as example of an “ingeniously simple and effective” argument, it took me more than 37 years to discover this simplification.