
One such sorting algorithm is Radix Sort, which was first used by Herman Hollerith for sorting punch cards in the 1890 census. Hollerith's tabulating machines were a tremendous success, leading to the founding of International Business Machines (IBM). But for Radix Sort to work, you have to know the maximum number of digits in any of the data; that's why it's not considered a general purpose sorting algorithm. However, on suitable data, Radix Sort has complexity of n×m where n is the number of items to be sorted and m the maximum numbers of digits.
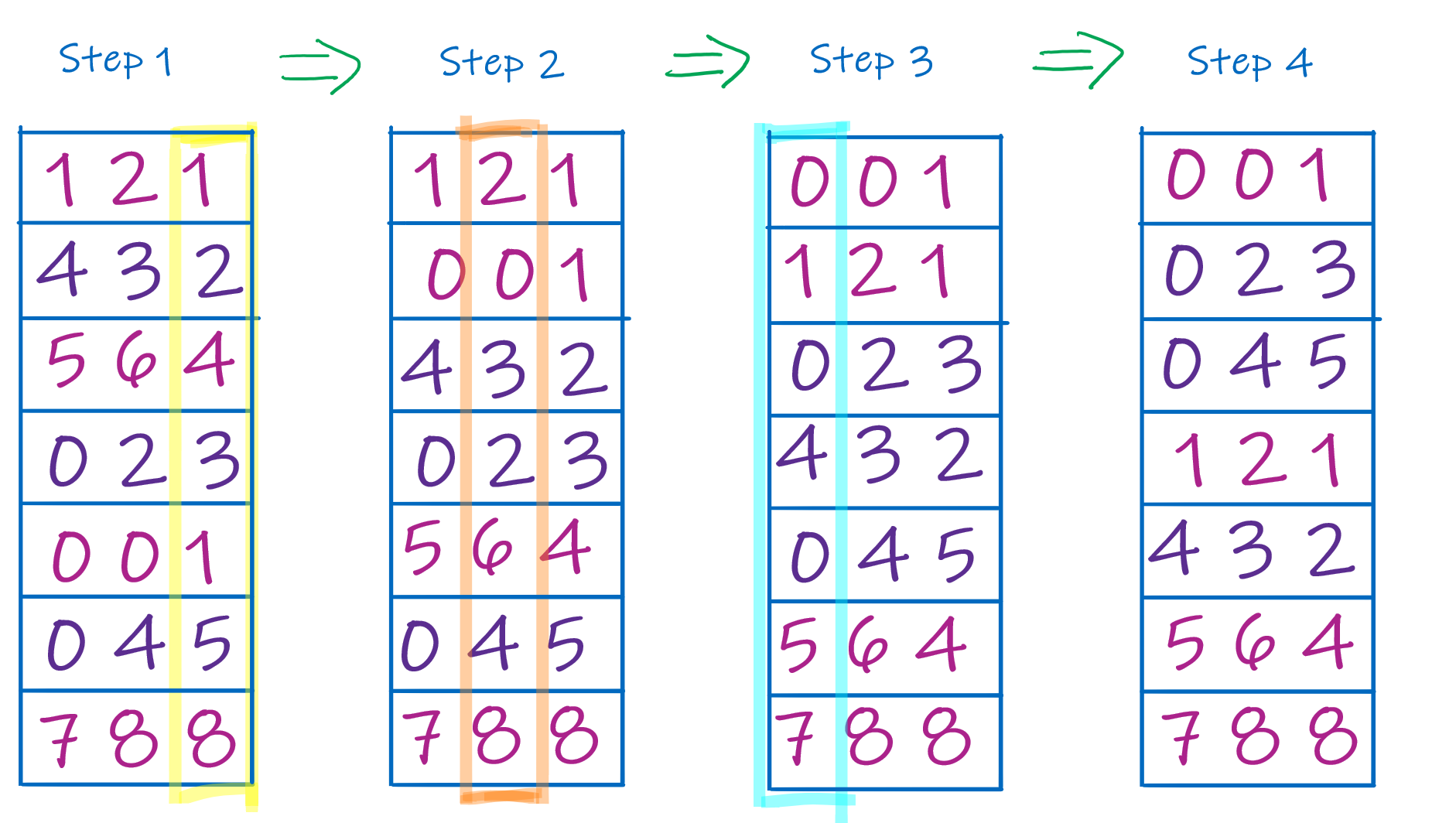
Let's look at an example to see how it works. Consider the following list of 20 non-negative integers in the range 0 to 999.
[200, 793, 355, 44, 893, 153, 12, 725, 958, 478, 214, 408, 836, 659, 224, 411, 299, 346, 590, 443]Now suppose we place them into a series of 10 lists ("buckets") according to their least significant (1's) digit. This would give us:
[[200, 590], # items ending in 0 [411], # ending in 1 [12], # ending in 2 [793, 893, 153, 443], # ... etc [44, 214, 224], [355, 725], [836, 346], [], [958, 478, 408], [659, 299]]If you were to "flatten" this out into a single list, you'd find that all of the items have now been sorted according to their last digit. This would give:
[200, 590, 411, 12, 793, 893, 153, 443, 44, 214, 224, 355, 725, 836, 346, 958, 478, 408, 659, 299]
Now take that list and perform again those same two steps, but this time using the 10's digit. (Be sure to treat the 10's digit as 0 it's only a one digit number.) That would give:
[[200, 408], [411, 12, 214], [224, 725], [836], [443, 44, 346], [153, 355, 958, 659], [], [478], [], [590, 793, 893, 299]]At this point everything is sorted according to the two least significant digits. Repeating one more time for the 100's digit would give:
[[12, 44], [153], [200, 214, 224, 299], [346, 355], [408, 411, 443, 478], [590], [659], [725, 793], [836, 893], [958]]with flattened version:
[12, 44, 153, 200, 214, 224, 299, 346, 355, 408, 411, 443, 478, 590, 659, 725, 793, 836, 893, 958]Notice that this is fully sorted. In general, given a list of integers of no more than k digits, k rounds of Radix Sort fully sort the list. (BTW: if you do more than k rounds, it shouldn't hurt anything; since those extra digits are all zero, it will just place all data items into the zero bucket. But it's a total waste of time!)
The algorithm is as follows:
Given a list Data to sort containing non-negative integers of at most n digits.
For rnd in range( n ):
Generate a list sortLists of 10 empty lists;
for each item in Data:
append item to sortList[d], where d is the rnd digit of item,
or d is 0 if item has no digit in the rnd position
flatten sortLists to generate a new version of Data
Return the final flattened list
Strictly speaking, you don't have to flatten after each round, but I
find it easier to see what's happening.
It's easy to generate a list of test data with the following code:
data = [ random.randint(0, 2**m-1) for i in range(numberOfValues) ]
You should have a "main" program with two parameters:
def radixSort( testData, rounds ):
# Given a list testData of random integers, none of more than rounds
# digits, use radix sort to sort them.
print( "\nInput data:" )
print( testData )
[your code to implement Radix Sort goes here]
print( "\nFinal sorted list:" )
print( finalSortedData )
# This is just for testing; it generates a list of 50 random integers
# between 0 and 999.
testData = [ random.randint(0, 999) for i in range(50) ]
rounds = 3
# This calls radixSort on the randomly generated test data for 3 rounds.
# It would be a good idea to test your code on different size data.
radixSort( testData, rounds )
The grading script will generate a new list of testData and a call to
your radixSort function; make sure that you call
it radixSort and that it has those two parameters.Be careful of the following: You might think you can generate a list of 10 empty lists as follows:
sortLists = [[]] * 10That does generate a list of 10 empty lists, but they're all the same list. You might get behavior such as this:
>>> sortLists = [[]] * 10 >>> sortLists[0].append( 123 ) >>> sortLists [[123], [123], [123], [123], [123], [123], [123], [123], [123], [123]]Instead use:
>>> sortLists = [ [] for i in range(10) ] >>> sortLists[0].append(123) >>> sortLists [[123], [], [], [], [], [], [], [], [], []]
I would strongly suggest that you define a function to get the kth digit of an integer. Treat the input as an integer; don't convert it to a string. I defined the following two functions for this:
def listOfDigits( num ):
# Given a non-negative integer num, return a list of its digits,
# from least to most significant.
...
def getDigit( num, k ):
# Given a list of digits, select the kth one, if any. Otherwise,
# return 0.
...
> python RadixSort.py Input data: [710, 242, 907, 845, 294, 46, 376, 256, 164, 163, 112, 787, 28, 15, 254, 322, 965, 127, 509, 352, 796, 880, 360, 543, 347, 234, 792, 960, 984, 938, 990, 746, 755, 883, 589, 855, 993, 966, 979, 785, 18, 373, 137, 944, 39, 521, 545, 928, 902, 949] Round: 0 [ [710, 880, 360, 960, 990] [521] [242, 112, 322, 352, 792, 902] [163, 543, 883, 993, 373] [294, 164, 254, 234, 984, 944] [845, 15, 965, 755, 855, 785, 545] [46, 376, 256, 796, 746, 966] [907, 787, 127, 347, 137] [28, 938, 18, 928] [509, 589, 979, 39, 949] ] Round: 1 [ [902, 907, 509] [710, 112, 15, 18] [521, 322, 127, 28, 928] [234, 137, 938, 39] [242, 543, 944, 845, 545, 46, 746, 347, 949] [352, 254, 755, 855, 256] [360, 960, 163, 164, 965, 966] [373, 376, 979] [880, 883, 984, 785, 787, 589] [990, 792, 993, 294, 796] ] Round: 2 [ [15, 18, 28, 39, 46] [112, 127, 137, 163, 164] [234, 242, 254, 256, 294] [322, 347, 352, 360, 373, 376] [] [509, 521, 543, 545, 589] [] [710, 746, 755, 785, 787, 792, 796] [845, 855, 880, 883] [902, 907, 928, 938, 944, 949, 960, 965, 966, 979, 984, 990, 993] ] Final sorted list: [15, 18, 28, 39, 46, 112, 127, 137, 163, 164, 234, 242, 254, 256, 294, 322, 347, 352, 360, 373, 376, 509, 521, 543, 545, 589, 710, 746, 755, 785, 787, 792, 796, 845, 855, 880, 883, 902, 907, 928, 938, 944, 949, 960, 965, 966, 979, 984, 990, 993] oscar:~/cs303e/python>
Your file must compile and run before submission. It must also contain a header with the following format:
# Assignment: HW10 # File: RadixSort.py # Student: # UT EID: # Course Name: CS303E # # Date: # Description of Program:

When testing a small program, you can usually come up with test data by hand. But when testing a larger program, particularly one that will be used by many people, it's important to be thorough in your testing. For some problems, it is even possible to test exhaustively, meaning to exercise all possible test cases. But that's rare; for even simple problems there are often just too many possibilities.
At very least, try to test many different categories of possible inputs, including edge cases, inputs that are near the boundary of legal inputs. For example, if your program expects an input that is non-negative, make sure to test what happens if the input is 0 and what happens if the program is provided an illegal negative input.
Higher order functions: Unlike a lot of programming languages, Python allows what are called higher order functions. That means that the arguments to a function don't have to be objects, but can be other functions. For example, consider the following definition:
def filter( lst, f ):
# Return a new list that contains exactly the
# elements of lst that satisfy predicate f.
ans = []
for e in lst:
if f( e ):
ans += [e]
return ans
Notice that the second argument is the name of a
function. filter returns the list of all of the elements of
the first argument that "satisfy" the predicate (boolean-valued
function) in the second argument position. Consider the following
predicates:
def isNegative (x):
# x is a negative number
return x < 0
def isGreaterThan10 (x):
# x is a number larger than 10
return x > 10
def isLCVowel (ch):
# ch is one of "a", "e", "i", "o", "u"
return ch in "aeiou"
Now I can filter any list for any predicate I care to define,
including those:
>>> from MyListFunctions import *
>>> lst4 = [1, -2, 3, -4, 5, -2.5, 0]
>>> filter( lst4, isNegative )
[-2, -4, -2.5]
>>> filter( lst4, isGreaterThan10 )
[]
>>> filter( [2, 4, 8, 16, 32, 64], isGreaterThan10 )
[16, 32, 64]
>>> filter( list("Who'd have thought it?"), isLCVowel )
['o', 'a', 'e', 'o', 'u', 'i']
Pretty cool, isn't it! Python has several higher order features built
in. We're not going to cover them this semester, but they make Python
very powerful.