CS303E Project 2: Spring 2024

Instructor: Dr. Bill Young
Due Date: Monday, April 8 at 11:59pm

Assignment (Implementing a Caesar Cipher)

In cryptography, a Caesar Cipher is one of the simplest and most widely known encryption techniques. It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number of positions down the alphabet. For example, with a right shift of 3, A would be replaced by D, B would become E, and so on. Letters near the end of the alphabet wrap around to the beginning, so X goes to A, Y goes to B, and Z goes to C. The cipher is named after Julius Caesar, who used it in his private correspondence.

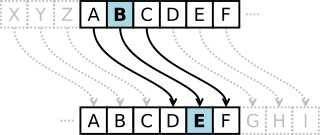
You should implement the Caesar Cipher with the ability to encrypt and decrypt. Specifically, write a program that performs the following steps:

Accept from the user a command: encrypt or decrypt. Case does not matter, so Encrypt, ENCRYPT, or even EnCrYpT is fine. Terminate with an error message if given any other command. Acknowledge a correct command. (See example below.)
Accept from the user a shift value, which should be an integer between 0 and 25. You can assume that the input is an integer, but must validate that the value is in the right range. Terminate with an error message if it's not.
Accept from the user a string to encrypt/decrypt.
Encrypt or decrypt (as requested) the text and display the result. Your program should preserve the case of letters and leave non-letters unchanged.

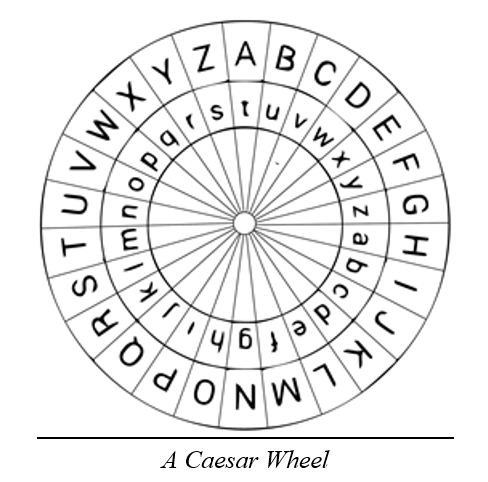How do you carry out the shifting? Consider an upper case letter in variable ltr. All upper case letters have ASCII codes from 65 to 90. You might think you could just add the shift value to the letter's ASCII code. But that wouldn't work if (ord(ltr) + shift) is greater than 90. We want that to wrap back around to the 65 end of the range.

Suppose variable ltr contains the letter you want to shift and variable shft contains the shift value. Then you only need to do the following steps. Why this works is explained in the Programming Tips section below.

   W = ord(ltr) - ord('A')        # shifts to range [0 .. 25]
   X = (W + shft) % 26            # (W + shift) modulo 26
   Y = X + ord('A)                # shift back to range [65 .. 90]
   Z = chr( Y )                   # what letter has that ASCII code?

Note that decryption is just encryption with a shift value of (26 - shft). For example, if shft is 10, then the negative shift is (26 - 10) or 16. (Note this means that you can use the same code for encrytion and decryption; just pass the shift value as a parameter.) Now all you have to do is to code this. Note that the corresponding code for lower case merely replaces 'A' with 'a'. You can either treat lower and upper case letters separately, or figure out how to do both with the same code (hint: put either 'A' or 'a' into another variable, depending on whether you're shifting uppercase or lowercase letters).

You can, and should, use any of the string methods we've covered in the class.

Expected Output:

Below are some runs of my program that show appropriate output, including responses to erroneous inputs. Mimic the prompts and error messages exactly.

> python Project2.py
Enter Caesar cipher command (encrypt/decrypt): What
Unrecognized command: what
> python Project2.py
Enter Caesar cipher command (encrypt/decrypt): EncrYPt
You've asked to encrypt.
Please enter shift value (0 .. 25): -14
Illegal shift value: -14
> python Project2.py
Enter Caesar cipher command (encrypt/decrypt): EnCrYpt
You've asked to encrypt.
Please enter shift value (0 .. 25): 3
Please enter text to encrypt: My dog has fleas; doesn't yours?
The encrypted text is: Pb grj kdv iohdv; grhvq'w brxuv?
> python Project2.py
Enter Caesar cipher command (encrypt/decrypt): DECRYpt
You've asked to decrypt.
Please enter shift value (0 .. 25): 3
Please enter text to decrypt: Pb grj kdv iohdv; grhvq'w brxuv?
The decrypted text is: My dog has fleas; doesn't yours?
>

Turning in the Assignment

The class should be in a file named Project2.py. Submit the file via Canvas before the deadline shown at the top of this page. Submit it to the assignment project2 under the assignments sections by uploading your python file.

Your file must compile and run before submission. It must also contain a header with the following format:

# File: Project2.py
# Student: 
# UT EID:
# Course Name: CS303E
# 
# Date:
# Description of Program:

Programming tips

Use functions: At this point in the semester, it shouldn't be necessary to say that you should use functions to code this. Below are the functions I defined in my implementation. You don't have to define exactly these functions, but you should use functional abstraction to build an understandable and maintainable program.

  shiftLetter( ch, baseChar, shiftValue ):
  shiftUpperCaseLetter( ch, shiftValue ):
  shiftLowerCaseLetter( ch, shiftValue ):
  caesarCipherText( text, shiftValue ):
  caesarCipher ():

Add robustness: I always find it a good idea to make any system I code as robust and user-friendly as possible. For example, I find it annoying when using a system to have to worry about the case of input commands. Why not make commands case insensitive so that "EnCRypt" works as well as "encrypt"? It's easy to do that; just lowercase the command entered by the user (using comm.lower()) and then compare that to the lowercase version. If they match, accept the command; otherwise, reject it.

Remember: if the command is stored in variable comm, comm.lower() doesn't change comm. You'd want to do something like:

   commLower = comm.lower()

if you need to preserve comm, to print an error message, for example. If you don't need to preserve comm, you can just do this:

   comm = comm.lower()

Modular arithmetic: In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" when reaching a certain value, called the modulus. You do modular arithmetic all the time, but you may not realize it. For example, if it's 10am and you want to know what time it will be in 4 hours, you're doing modular arithmetic, because the time wraps back to 0 every 12 hours.

The remainder operator % is how you compute this. For any starting time start and increment inc, you compute the new time as: (start + inc) % 12. For example, 4 hours after 10am is (10 + 4) % 12 == 2. It's so simple that you probably do it unconsciously. But suppose it's 10am and you want to know what time it will be in 12,725 hours. The same trick works: (10 + 12725) % 12) == 3, so it will be 3:00. (Note we don't actually know whether that's 3am or 3pm. To do figure that, we could use 24 hour time: (10 + 12725) % 24 == 15, so it would be 15:00 or 3pm.)

Note that this only works if the numbering starts at 0. When we applied modular arithmetic to the ASCII codes for upper case numbers in the Caesar Cipher case that wasn't the case; the codes were in the range 65 to 90, not 0 to 25. To compensate, we shifted all the numbers down by 65; that's why we subtracted by ord('A'). That meant that 'A' had a shifted value of 0; 'B' a shifted value of 1, etc. Next, we did the modular arithmetic on the shifted values. Finally, we shifted the result back up to the original range by adding ord('A').

If shft contains the shift value for encryption, then (26 - shft) is the shift value for decryption. Why is that? Shouldn't you just subtract shft to get back where you started? Yes, you can do that. But it turns out that (- shft) % 26 is equal to (26 - shft) % 26. Suppose that the shft contains 10. Then (26 - 10) is 16. So you'd encrypt by adding 10 to every letter (modulo 26). To get back to where you started, you could either subtract 10 or add 16, because adding 10 (to encrypt) and 16 (to decrypt) means adding a 26 total. But 26 means going all of the way around the circle back to where you started.