
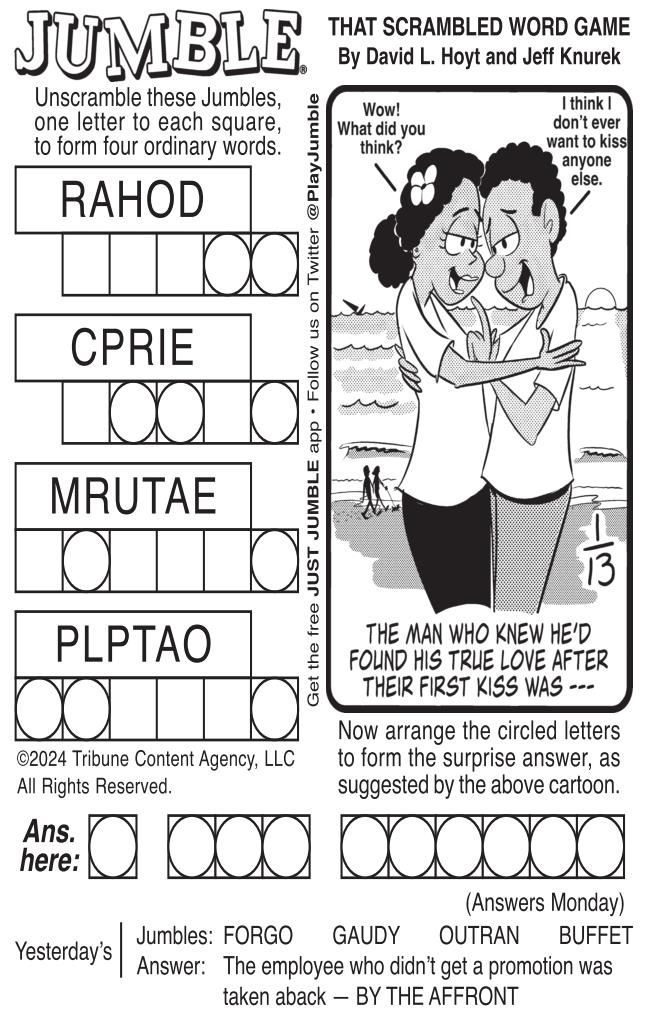




All scrambled words in Jumble are either 5 or 6 letters long. In this assignment you'll write a utility that would help you solve Jumbles. It should allow you to input a scrambled word and return the corresponding English word. This is a great example of a search problem. Given a scambled word and a database of English language words, search the database to find one (or more) words that have exactly the same letters, but in different order.
We're going to use a particular approach called hashing for creating the database and searching it for matches. We'll first briefly outline the idea of hashing and then explain how we'll use it to solve this problem.
Optimally, it would be nice if the colors were evenly distributed so that each bucket had approximately the same number of candies. For example, if all of the M&Ms in the bag were red, this scheme wouldn't be any better than linear search. Also, it would be nice if there were many different colors, so that each bucket only had a small number of candies in it.
That is the basic idea of hashing: Find a "hash function" that you can apply to all items in the search space to pre-sort them into various "buckets." Then whenever you need to find a specific value, apply the hash function to that value. That should tell you what bucket to search. If the item is present, it must be in that bucket. Assuming that the buckets all contain approximately the same small number of items, this is a very efficient search strategy.
Define the hash function: To make this approach work for our Jumble problem we need a hash function hash( s ) that works on ASCII strings. (Note that our actual hash function has two parameters, but we could have made the second one a global variable.) We'll assume that it maps strings to non-negative integers; those are the 'hash values.' The hash value of a given string is an index into a collection of buckets; if present, the string will be in the bucket with that index.
We apply the hash function to all of the items in our search space (the words in our wordlist). For each item, we put it into a bucket associated with its hash value. We'll do this with a dictionary. Each key in the dictionary is a non-negative integer. The value associated with that key is a list of all words in the wordlist that have that key as their hash value. That will be our database.
Let's illustrate this with a concrete example. Suppose we're attempting to find an English word that's an angram of "bnedl" (the first Jumble in the first panel shown above). We apply our hash function to that string. Suppose the result is 7269. We look in the 'bucket' associated with key 7269 in dictionary. In that bucket is a list of all English words from our wordlist that have hash value 7269. Hopefully, that list is pretty short and we can search it linearly for any word with the same 5 letters as 'bnedl'. We find and report 'blend'.
Note that our hash function must be such that the value returned is invariant under permutations of the letters in the string. For example, "bnedl" and "blend" must give the same hash value. That ensures that taking the hash value of the scrambled version ('bnedl') will take us to the "bucket" containing the unscrambled word ('blend').
Devising an effective hash function is something of an art. For our purposes, we'll define a function hash( s ) as follows. PRIMES below is a list of the first 30 primes:
PRIMES = [ 2, 3, 5, 7, 11, 13, 17, 19, 23, 29,
31, 37, 41, 43, 47, 53, 59, 61, 67, 71,
73, 79, 83, 89, 97, 101, 103, 107, 109, 113 ]
For a given ASCII string s, lowercase it so that you only need deal
with lowercase letters. For each letter in the string, take the
0-based index of the letter in the alphabet: 'a' is the 0th letter;
'b' is the 1st letter; 'c' is the 2nd letter; etc. Then take the
corresponding prime from the list above: 'a' goes to 2; 'b' goes to 3;
'c' goes to 5; etc. Multiply those primes together. Finally, return
the product mod 10007; that is, return the remainder when dividing the
product by 10007 (i.e., product % 10007).Here's an example: let the input string be 'python'. 'p' is letter 15 in the 0-based alphabet; 'y' is letter 24; 't' is letter 19; 'h' is 7; 'o' is 14; and 'n' is 13. Corresponding to 'p' (letter 15) is the 15th (0-based) prime, 53. For 'y' we have the 24th prime, 97. The other primes are 71, 19, 47, 43. Multiply those 6 primes together to get 14,016,057,389. Finally, take (14016057389 % 10007) or 3014.
>>> hash( "python", 10007 ) 3014 >>> hash( "abacus", 10007 ) 3257 >>>Notice that, as needed, hash is invariant over reordering the letters in a string. Think about why that is? Setting the modulus to 10007 was an arbitrary choice. For technical reasons, the modulus should be a prime. After experimenting, I found 10007 to give good overall performance. It yields potentially 10007 different buckets, which spreads the data widely and means specific buckets contain relatively fewer items.
Create the database(s): To build our database, we'll need a file of English language words. Accept the file name from the user and check that it exists. Here's the file to use when testing your code: wordlist file. Download that file into the same directory as your program. This file contains many English words, including some very weird words. The words in the file are alphabetically ordered, but that won't really matter. Read words from the file one line at a time; there's one word per line. Don't read the entire file at once. For each word, check the length. Discard any that aren't of length 5 or 6.
You will build two dictionaries, one for words of length 5 and one for words of length 6. (I'll call them dict5 and dict6.) Store words of length 5 in dict5 and words of length 6 in dict6, as follows. Say the word is "abacus". We noted above that "abacus" has hash value 3257. You'd store "abacus" in the value (list) associated with key 3257 in dict6. I.e., if that list is not empty, append "abacus" to dict6[3257]; otherwise, set dict6[3257] to ["abacus"]. You should have a function
createDicts( filename )that creates and returns the two dictionaries, along with printing the report described directly below.
You will also print a report on building the dictionaries. This should report the name of the wordlist file from which the build occurs, the total number of words read, the number of words of length 5, the size of the resulting dict5 (i.e., len(dict5)), the number of words of length 6, and the size of the resulting dict6. Here's what this should look like (including the surrounding prompts):
> python Jumble.py Creating dictionaries from file: wordslist Total words found: 113810 Words of length 5: 8258 Dictionary(5) buckets: 4592 Words of length 6: 14375 Dictionary(6) buckets: 6873 Enter a scrambled word (or EXIT): ...BTW: we noted above that we'd like to divide our database words as evenly as possible into some number of "buckets." The number of potential buckets is determined by the modulus (there are exactly k possible results from n % k). More buckets means fewer items in each bucket, which means a faster search. But there's a limit. I tried varying the modulus across a wide range of values. Consider the following statistics:
| Modulus | Dict5 Size | Dict5 Max Bucket | Dict6 Size | Dict6 Max Bucket |
| 503 | 502 | 37 | 502 | 50 |
| 1009 | 1008 | 22 | 1008 | 32 |
| 10007 | 4592 | 15 | 8857 | 12 |
| 100003 | 5906 | 11 | 10786 | 11 |
| 1000003 | 6045 | 11 | 11300 | 12 |
It is no accident that the smallest bucket size for dict5 is 11 no matter how big we make the modulus. Recall that some strings have multiple permutations all of which are English language words. If our program is going to work, those all have to be in the same bucket. For example, the following words all appear in our file: 'apers', 'asper', 'pares', 'parse', 'pears', 'prase', 'presa', 'rapes', 'reaps', 'spare', 'spear'. Notice that they all have exactly the same letters, hence the same hash value. Consequently it would be impossible to find a hash function for this problem for which the largest bucket was smaller than 11. So our choice of hash function and modulus is pretty good. A larger modulus might make the average bucket size slightly smaller, but it wouldn't make a significant difference.
Loop to accept and solve jumbles: In your main() program, first create the two dictionaries. Then accept strings from the user; each string is a jumble. If the user enters "EXIT" print a goodbye message and exit. If the string contains illegal characters or is not of length 5 or 6, print an error message and continue. Otherwise, accept the word, hash it to obtain a hash value num, and check if there are words in the dictionary at key num that contain exactly the same letters; return that as the solution. If there is no solution, say so. Then continue to accept another string from the user.
Note that there could be multiple solutions, since there are many English words with the same letters (e.g, 'downer' and 'wonder'). However, the authors of Jumble take care that none of the scrambles they use have multiple possible answers. So it's OK to return the first answer you find.
You should print out the solution, if you find one, following the sample output below. Also, print out the number of comparisons you made. You'll go directly to the hash bucket (list) of potential matches and then count how many of those you checked before you found a match or had tried them all.
Finally, let's see how long it took to solve each jumble. Do that with the following code:
import time # put this at the top of the module
...
start = time.time() # set the timer, save start time
< code to attempt to solve the jumble >
end = time.time() # stop the time, save end time
# Print out the time stats on this attempt.
print("Solving this jumble took %2.5f seconds" % (end - start))
Hint 1: There are various ways to check whether two strings
contain the same letters. The string function sorted(s)
returns a sorted list of the characters in s. So two strings s1 and
s2 contain the same letters if sorted(s1) == sorted(s2).Hint 2: As usual, make your program robust. Strip extra whitespace from user supplied values. Don't make your program depend on the case of user input. Perhaps allow alternatives (such as 'halt' instead of 'exit'.)
> python Jumble.py Creating dictionaries from file: wordslist Total words found: 113810 Words of length 5: 8258 Dictionary(5) buckets: 4592 Words of length 6: 14375 Dictionary(6) buckets: 6873 Enter a scrambled word (or EXIT): xy#$@! Word contains illegal characters. Try again Enter a scrambled word (or EXIT): xyz Word must be 5 or 6 characters long. Try again Enter a scrambled word (or EXIT): abcdefgh Word must be 5 or 6 characters long. Try again Enter a scrambled word (or EXIT): abcdef Sorry. I can't solve this jumble! Try again. Solving this jumble took 0.00013 seconds Made 4 comparisons. Enter a scrambled word (or EXIT): bnedl Found word: blend Solving this jumble took 0.00008 seconds Made 1 comparisons. Enter a scrambled word (or EXIT): idova Found word: avoid Solving this jumble took 0.00013 seconds Made 1 comparisons. Enter a scrambled word (or EXIT): seheyc Found word: cheesy Solving this jumble took 0.00007 seconds Made 2 comparisons. Enter a scrambled word (or EXIT): aracem Found word: camera Solving this jumble took 0.00006 seconds Made 1 comparisons. Enter a scrambled word (or EXIT): exit Thanks for playing! Goodbye. >It is strongly suggested that you test your code on the scrambled words from that day's Jumble:Today's Jumble.
Your file must compile and run before submission. It must also contain a header with the following format:
# Assignment: Project3 # File: Project3.py # Student: # UT EID: # Course Name: CS303E # # Date Created: # Description of Program:

In Python, there isn't a default entry point. If you want to start executing by calling main you have to have an explicit call main(). But since you are telling the system where to begin executing, you can call any function you like. For this project, I called my "main" function solveJumbles.
def solveJumbles( ):
...
Searching: Attempting to find one item in a large collection of
items is a very important application area in computing. For example
in the course lectures we talked about linear search as opposed to
binary search. Both have their place. If the collection is unordered
or unorderable, linear search may be the best you can do. That
requires searching about half the items, on average, if the item is
present, and all of the items if it's not present. Considering that
the search space of this Jumble problem (around 114,000 items in the
wordlist), that's pretty slow.Binary search would cut the average to around 17 comparisons per search (for a search space of 114,000 items); but it's not clear how you could even do binary search for this problem, since you don't know in advance what you're looking for. One could find all n! (factorial of n) permutations of a string of length n and then do binary search for each item in the list. For a 6-character string, that's 6! * 17 = 720 * 17 = 12240 comparisons. Ouch!
The efficiency of hashing depends critically on the nature of the problem and of the hash function chosen. But you can see that after the (linear) work of setting up the dictionaries initially, each search takes only a very few comparisons. It's a very useful technique to add to your toolkit.