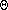Lecture 4

Asymptotic Notation continued

Here are two more forms of asypmtotic notation:

Loose Upper Bounds: Little-o

Little-o is a "loose" upper bound. If f(n) = o(g(n)) then g grows strictly faster than f; you can multiply g by any positive constant c and g will still eventually exceed f. Here is the formal definition:

o(g(n)) = { the set of all f such that for any positive constant c there exists a positive constant n₀ satisfying 0 <= f(n) <= cg(n) for all n >= n₀ }.

So, for example, n² is o(n³) but not o(n²).

Since g always grows strictly faster than f, we have

f(n) = o(g(n)) implies lim_n->oo (f(n)/g(n)) = 0.

If g is asyptotically non-negative, the implication will also run the other way, i.e., if the limit is 0, then f(n) = o(g(n)) is true.

Loose Lower Bounds: Little-omega

Little-omega (represented mercifully here by the letter 'w') is the "loose" analog to big-Omega. It is a loose lower bound in the same way little-o is a loose upper bound:

w(g(n)) = { the set of all f such that for any positive constant c there exists a positive constant n₀ satisfying 0 <= f(n) <= cg(n) for all n >= n₀ }.

So, for example, n³ is w(n²) but not w(n³).

As before, since f always grows strictly faster than g, we have

f(n) = o(g(n)) implies lim_n->oo (g(n)/f(n)) = 0.

Common Mathematical Facts for Analysis of Algorithms

Certain mathematical concepts come up frequently in the analysis of algorithms. We will see more of these as they come up in algorithms, but let's look at an overview for now (your book goes into more detail here; you should read section 2.2):

Monotonicity. A function f is monotonically increasing if n <= m implies f(n) <= f(m). Many of the functions that describe running times of algorithms are monotonically increasing.
Polynomials. A polynomial is a sum of terms, each of which are are constant coefficients multiplied by some power of the dependent variable (usually n). For example, 3n³ - 2n² + 6n + 12. Polynomials often describe the running times of algorithms. The degree of a polynomial is the highest exponent the variable is raised in any of the terms. Any polynomial of degree k is in (n^k). This is true even if the lower order terms are multiplied by something in o(n), such as log n (Is this true if we replace o with O?).
Exponentials. An exponential is a constant base raised to a variable power. Exponentials sometimes describe the running times of algorithms, but since an exponential grows very quickly, these algorithms are of limited use. Exponentials and their properties can be used to help analyze an algorithm, as we saw with merge sort. Some properties:
- a⁰ = 1
- a^{- n} = 1/aⁿ
- (aⁿ)^m = a^mn
- aⁿa^m = a^n+m
Polynomials are preferred to exponentials as running times because any polynomial will always grow more slowly than any exponential since n^k = o((1 + )ⁿ) for any positive . Your book has a nice proof of this using limits.
Logarithms. A logarithm of a number x with respect to a base a is the number you have to raise a to to get x. So if y = log_ax then a^y = x. Logarithms are thus the opposites of exponentials. They describe the running times of some algorithms. Logarithmic time is much faster (i.e., the running time grows more slowly as a function of n) than linear or other polynomial time, so is very desirable. Many divide-and-conquer algorithms such as merge sort or binary search have a logarithmic term in their running times because you can only subdivide a set of n things into two equal parts log₂n times.
Some logarithms are use more frequently:
- log_ex, or natural logarithm. This is usually written as ln x. e is one of those transcendental numbers like pi that come up frequently in mathematics; natural logarithm is often easier to work with so is often preferred.
- log₂x. The logarithm base two comes up often in divide-and-conquer algorithms and other areas of computer science. For example, the number of bits required to store a number n in binary is log₂n.
- log₁₀x. Log base ten of a number is one less than the number of decimal digits in that number. It gives you an idea of the order of magnitude of a number. Basically, it only comes up because we are used to using a decimal (base 10) number system.
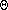Logs have some nice properties that are also described in your book. One in particular makes our choice of logarithm unimportant: log_ax = ln x / ln a. This means that every logarithm differs from every other logarithm only by a constant, so we always have log_an = (ln n).