Subsection 1.1.3 Logical Doesn't Mean Long or Complicated
Some problems are hard and solutions to them are long and complicated. This can happen even when the problem appears simple.
Activity 1.1.1.
Consider any plane (flat surface). Divide it into regions. Call this a map. Now color the map’s regions, following one rule: Any pair of regions that touch at more than a single point cannot be the same color.
What’s the largest number of colors that might be required to color a map?
The Four Color Theorem asserts that it is always possible to color a map in no more than four colors. The theorem is known to have been conjectured as early as 1852. But the first generally accepted proof of it wasn’t published until 1977. And it took the help of a computer to construct.
Yet other problems have simple and elegant solutions, even if those solutions aren’t immediately obvious.
Activity 1.1.2.
A single elimination tournament determines a winner on the basis of matches. In each match there is exactly one winner and one loser. Any team losing a match immediately leaves the tournament. The winner is the single team that remains after all others have lost. (Notice that there is no assumption about the structure of the games. There could be seedings, a ladder, a balanced tree, or other structures employed.) Suppose that there are 17 teams. How many matches must be played in order to determine a winner?
Problems 1.1.3.
(a)
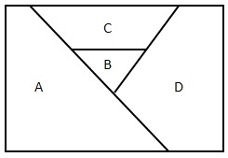
Consider this map:

How many colors are required to color it?
(b)
Consider this map:
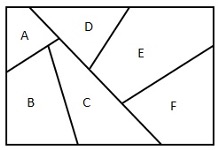
How many colors are required to color it?
(c)
How many matches must be played in a single elimination tournament with 17 teams?
