CS 343
Homework 5
You
may do this assignment either by yourself or in a team of up to three. It's sufficient to turn in one paper for your
team.
1.
Choose one of the following problems:
·
Wolf, Sheep, Cabbage (http://www.plastelina.net/games/game1.html)
·
Missionaries and Cannibals (http://www.plastelina.net/games/game2.html)
·
Family Crossing (http://www.plastelina.net/games/game3.html)
a) Play the game.
c) Describe the problem as a state space search.
d) Which search algorithm works best for solving the
problem?
2.
Consider the class of cryptarithmetic problems, in
which an arithmetic problem is represented in letters, as shown in the examples
below. The task is to assign a digit to
each letter in such a way that the answer to the problem is correct. If the same letter occurs more than once, it
must be assigned the same digit each time.
No two different letters may be assigned the same digit.
SEND DONALD CROSS
+ MORE +
GERALD + ROADS
MONEY ROBERT DANGER
a) Pick at least one of these problems and solve it.
b) Describe cryptarithmetic
as a state space search problem.
3. (R & N 3.5) Consider
the n-queens problem using the
"efficient" incremental formulation given on page 67. Explain why the state space size is at least
. Estimate the largest n for which exhaustive exploration is feasible. (Hint: Derive a lower bound on the branching factor
by considering the maximum number of squares that a queen can attack in any
column.)
4.
(R & N 3.8) Consider a state space where the start state is number 1 and
the successor function for state n returns two states, number 2n and 2n + 1.
a) Draw the portion of the state space for states 1
to 15.
b) Suppose the goal state is 11. List the order in which nodes will be visited
for breath-first search, depth-limited search with limit 3, and iterative
deepening search.
c) Would bidirectional search be appropriate for
this problem? If so, describe in detail
how it would work.
d) What is the branching factor in each direction of
the bidirectional search?
e) Does he answer to c) suggest a reformulation of
the problem that would allow you to solve the problem of getting from state 1
to a given goal state with almost no search?
5.
(R & N 3.13) Describe a state space in which iterative deepening search
performs much worse than depth-first search (for example, O(n2) vs. O(n)).
6.
(R & N 3.17) On page 62, we said that we would not
consider problems with negative path costs.
In this exercise, we explore this in more depth.
a) Suppose that actions can have arbitrarily large
negative costs; explain why this possibility would force any optimal algorithm
to explore the entire state space.
b) Does it help if we insist that step costs must be
greater than or equal to some negative constant c? Consider both trees and
graphs.
c) Suppose that there is a set of operators that
form a loop, so that executing the set in some order results in no net change
to the state. If all of these operators have negative cost, what does this
imply about the optimal behavior for an agent in such an environment?
d) One can easily imagine operators with high
negative cost, even in domains such as route finding. For example, some stretches of road might
have such beautiful scenery as to far outweigh the normal costs in terms of
time and fuel. Explain, in precise
terms, within the context of state-space search, why humans do not drive round
scenic loops indefinitely, and explain how to define the state space and
operators for route finding so that artificial agents can also avoid looping.
e) Can you think of a real domain in which step
costs are such as to cause looping?
7. (R&N 4.1) Trace the operation of the A*
search algorithm applied to the problem of getting to
8. (R&N 4.5) We saw on page 96 that the
straight-line distance heuristic leads greedy best-first search astray on the
problem of going from Iasi to Faaras. However, the heuristic is perfect on the
opposite problem: going from Fagaras to
9. Consider the Traveling Salesperson Problem: You are given a map that shows the roads that
connect a set of cities. Each segment of
road, from city A to city B, is labeled with its length in miles. You are also given a set of cities C and a
start city S. You must find the shortest
route from S back to itself that visits each city in C exactly once.
a) Show how branch and bound
can be used to solve this problem. Why
is it better than simple exhaustive search?
b) How much better is it?
10. (R&K3.8) In step
2(a) of the AO* algorithm, a random state at the end of the current best path
is chosen for expansion. But there are
heuristics that can be used to influence this choice. For example, it may make sense to choose the
state whose current cost estimate is the lowest. The argument for this is that, for such
nodes, only a few steps are required before either a solution is found or a
revised cost estimate is produced. With
nodes whose current cost estimate is large, on the other hand, many steps may
be required before any new information is obtained. How would the algorithm have to be changed to
implement this state-selection heuristic?
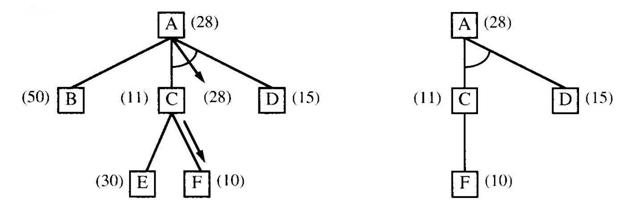
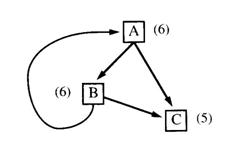
11. (R&K 3.9) The backward cost propagation step 2(c) of the AO* algorithm
must be guaranteed to terminate even on graphs containing cycles. How can we guarantee that it does? To help answer this question, consider what
happens for the following two graphs, assuming in each case that node F is
expanded next and that its only successor is A:
Also consider what happens
in the following graph if the cost of node C is changed to 3:
12. Consider the n-
13. (R & N 4.11) Give the name of the algorithm
that results from each of the following special cases:
a) Local beam search with k =
1.
b) Local beam search with one
initial state and no limit on the number of states retained.
c) Simulated annealing with T =
0 at all times (and omitting the termination test).
d) Genetic algorithm with
population size N = 1.
14. (R&N 4.14) Suppose that an agent is in a 3x3
maze environment like the one shown here.
The agent knows that its initial location is (1,1),
that the goal is at (3,3), and that the four actions, Up, Down, Left, Right have their usual effects unless blocked by a wall. The agent does not know where the internal
walls are. In any given state, the agent
perceives the set of legal actions; it can also tell whether the state is one
that it has visited before or a new state.
a)
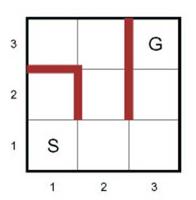
Explain how this
online search can be viewed as an offline search in belief state space, where
the initial belief state includes all possible environment configurations. How large is the initial belief space? How large is the space of belief states?
b) How many distinct percepts
are possible in the initial state?
c) Describe the first few
branches of a contingency plan for this problem. How large (roughly) is the complete
plan? Notice that this contingency plan
is a solution for every possible
environment fitting the given description. Therefore, interleaving of search and
execution is not strictly necessary even in unknown environments.