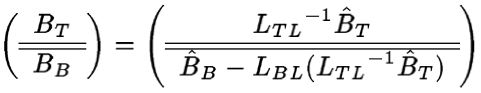Step 3: Determine the Loop-guard

Next, we determine the condition that determines when the final result has not yet been computed. In other words, the condition under which the loop continues to be executed. This condition is called the loop-guard, G .

Notice that when the loop is exited, we require the invariant to be true while clearly the loop-guard must be false. We also require that the final result has been computed. This means that the predicate

( Pinv &and ¬ G ) &rArr Ppost

must be true. If we now substitute the loop-invariant Pinv and post-condition Ppost into this predicate we find that we must find a condition G that makes

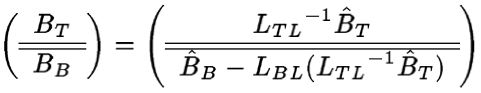( &and ¬ G ) &rArr

true.

Notice that if submatrix LTL consists of all of L then

  1. LBL consists of no rows,
  2. LBR is 0 × 0 ,
  3. BT consists of all of B (since L and B must be partitioned conformally),
  4. BB contains no rows,
  5. B&circT consists of all of B&circ (since L and B must be partitioned conformally), and
    6. B&circB contains no rows.
From these observations we conclude that

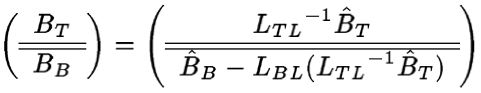( &and ( LTL = L ) ) &rArr

is true so that we pick G as G: ¬ ( LTL = L ) which we will write as the condition

G: ( m( LTL ) &ne m( L ) )

where m(X) returns the row dimension of matrix X.

[ UPDATE SOURCE ] [ VIEW PDF PS ]

[ BACK ] [ NEXT ]