Everything's Bigger in Texas
This page provides access to results, proofs and tools on ``the largest math proof ever" presented in the
SAT 2016 paper
Solving and Verifying the boolean Pythagorean Triples problem via Cube-and-Conquer
by Marijn J.H. Heule,
Oliver Kullmann, and
Victor Marek (best paper award). A preprint
is available on arXiv.
Introduction for the general public
The following question, known as the Boolean Pythagorean Triples problem, is a typical example of Ramsey Theory, and was asked by Ronald Graham in the 1980s and desribed below.First a definition: A Pythagorean Triple are three natural numbers 1 <= a <= b <= c, such that a2 + b2 = c2 holds. For example 3, 4, 5 is such a triple, since 32 + 42 = 9 + 16 = 25 = 52. While 2, 3, 4 is not such a triple, since 22 + 32 = 4 + 9 = 13 and 42 = 16. We note here that only natural numbers are considered, and thus 2, 3 can not be extended to Pythagorean triple (since 13 is not the square of some integer).
Now the question: Can we colour the natural numbers 1, 2, 3, ... with two colours, say blue and red, such that there is no monochromatic Pythagorean triple? In other words, is it possible to give every natural number one of the colours blue or red, such that for every Pythagorean triple a, b, c at least one of a, b, c is blue, and at least one of a, b, c is red ? We prove: The answer is No. That is easier to express positively: Whenever we colour the natural numbers blue or red, there must exist a monochromatic triple (one blue triple or one red triple).
More precisely we prove, using "bi-colouring" for colouring blue or red: 1) However we bi-colour the numbers 1, ..., 7825, there must exist a monochromatic Pythagorean triple. 2) While there exists a bi-colouring of 1, ..., 7824, such that no Pythagorean triple is monochromatic. Part 2) is relatively easy. Part 1) is the real hard thing -- every number from 1, ..., 7825 gets one of two possible colours, so altogether there are 27825 possible colourings, which all in a sense need to be considered, and need to be excluded. What is 27825? It is approximately 3.63 * 102355, that is, a number with 2356 decimal places. The number of particles in the universe is at most 10100, a tiny number with just 100 decimal places (in comparison).
Now let's perform real brute-force, running through all the possibilities, one after another: Even if we could place on every particle in the universe a super-computer, and they all would work perfectly together for the whole lifetime of the universe -- by far not enough. Even not if inside every particle we could place a whole universe. Even if each particle in the inner universe becomes again itself a universe, with every particle carrying a super-computer, still by far not enough. Hope you get the idea -- the $100 we got wouldn't pay that energy bill.
Fortunately there comes SAT solving to the rescue, which actually is really good with such tasks -- it can solve some such task and even more monstrous tasks. Our ``brute-reasoning'' approach solved the problem and resulted into a 200 terabytes proof -- the largest math proof ever. Though we must emphasise that this is in no way guaranteed, and possibly it will take aeons! SAT solving uses propositional logic, in the special form of CNF (conjunctive normal form). Fortunately, in this case it is easy to represent our problem in this form.
Extremal Partitions without Pythagorean Triples
Encoding
SAT encoding of partitioning {1, ..., n} into two sets such that no set contains a Pythagorean Triple.
- Ptn-encode, generates formulas encoding the boolean Pythagorean Triples problem. Ptn-encode has one mandatory paramemter n that limits the triples that are generated: only all triples (a, b, c) with a <= b <= c <= n.
- plain7824.cnf (highest occurring variable: 7820)
- plain7825.cnf
Reduced Formula
Blocked clause elimination (BCE), a SAT preprocessing technique, can significantly reduce the original encoding. BCE results in the following formulas:
- bce7824.cnf (226 kb, plain7824.cnf after blocked clause elimination)
- bce7825.cnf (226 kb, plain7825.cnf after blocked clause elimination)
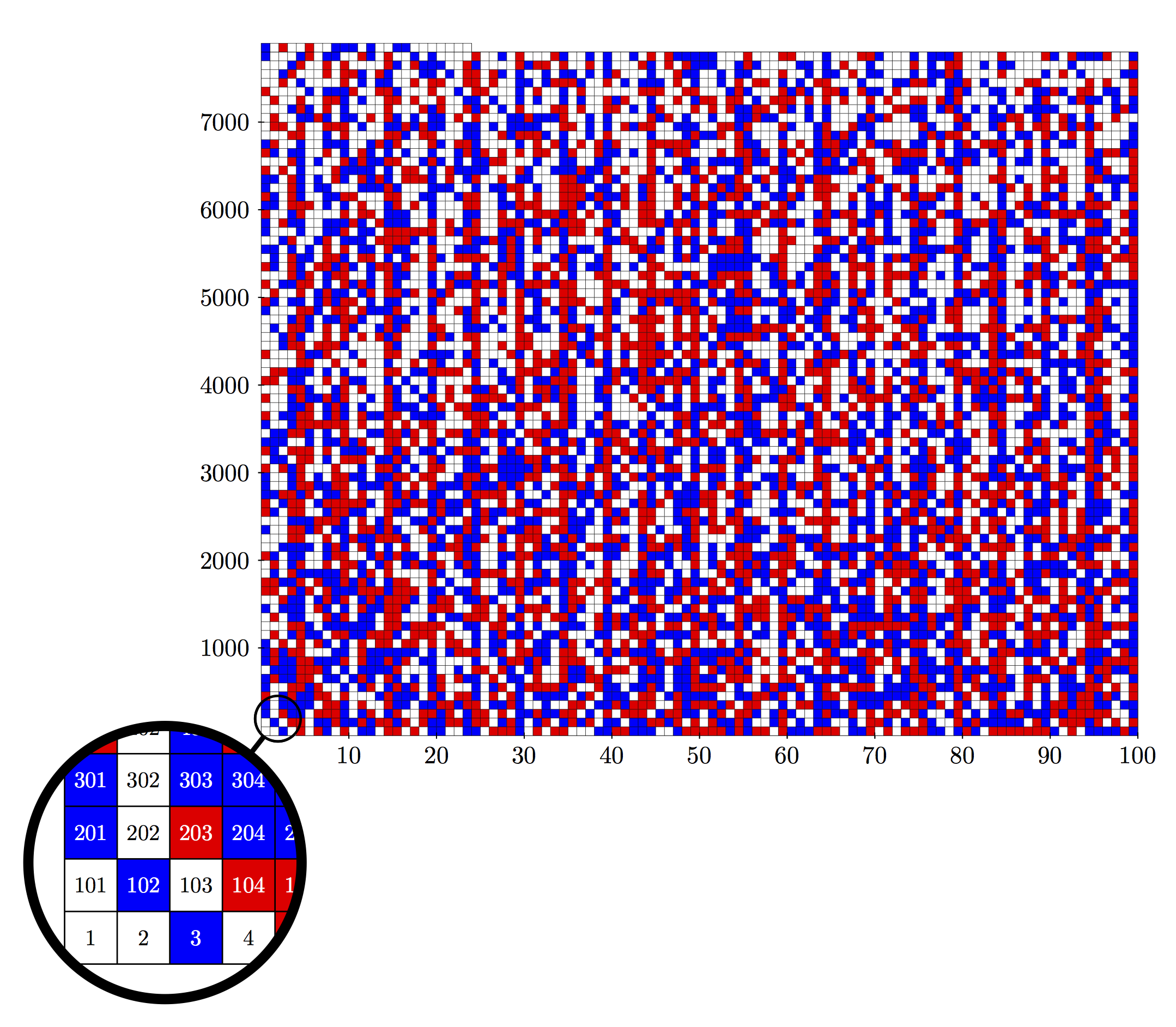
Extremal Partition
Below a visualization is shown of an extremal partition, i.e., a partitioning of {1, ..., 7824} into two sets, such that no set has a Pythagorean Triple. The image consists of three colors: red cells are in one set, while blue cells are in the other set. White cells are unconstrained: they can be in both sets without introducing a Pythagorean Triple.
Backbone
A variable occurs in the backbone of a formula if it is assigned to the same truth value in all solutions. The backbone of plain7824.cnf after symmetry breaking (i.e., adding unit clause "2520 0") is backbone7824.cnf (336 kb, including the formula).
Proof Parts
Original formula
The proof starts with a propositional formula that encodes the Pythagorean Triples problem using the above encoding using a variable offset of 10000 to allow symmetry-breaking techniques. This formula (407 kb) expressing partitioning {10001, ...., 17825} into two sets without one set having a Pythagorean Triple. Below, a short description is provided of the three proof parts, which can simply be merged by concatenation.
Transformation proof (part I)
The original formula is transformed, expressed in the first part of the proof transform.drat (2 mb), using blocked clause elimination and symmetry breaking to optimize the formula, resulting in transformed.cnf (262 kb). This transfomed formula is equal to bce7825.cnf with an additional unit clause to break the set symmetry.
Summarized cube proof (part II)
For each cube in the partition, the summarized cube proof cubes.drat (127 mb), contains a clause that is the negation of the cube. Adding a header to that proofs results in an unsatisfiable formula cubes.cnf (127 mb) which is the same as the million.cubes, but with all signs flipped).Proof of tautological property (part III)
The final part of the proof validates that the cube partition covers the entire search space. The cube partition can be viewed as a binary search-tree with the cubes as leaf nodes of this tree. For each internal node of this tree, the tautology proof tautology.drat (365 mb) contains a resolvent of its two children. The proof terminates with the empty clause.Cubes
Top Level Partition
Our partitioning of the transformed formula uses two levels. The first level consists of a million cubes, million.cubes (129 mb), expressed in the inccnf format.
Second Level Partition
The cube files of the second level of the partition are located at TACC. Each tar file consists of 1000 compressed cubes files. In order to produce the DRAT proof files, the following tools are required:
- The cubes files are compressed. To decompress the cubes files, first run bunzip2 on the
a*.bz2 files in the archive. Second further decompress the cubes with
cube-decode.c, which can simply be compiled with
gcc cube-decode.c -O2 -o cube-decode. - A modified version of glucose 3.0, called iGlucose, which accepts inccnf files as input.
Log files
The results (71 mb) of solving and validating the second level subproblems using range {1..7824}. Notice that only one cube (343864) is SATISFIABLE. The columns show the following information:- cube number;
- cube length;
- cube (split) time;
- conquer time;
- result;
- verification result;
- verification time; and
- size of DRAT proof .
In the Media
Selected articles on ``largest math proof ever":- I Programmer: A Mathematical Proof Takes 200 Terabytes To State. May 10, 2016
- Unocero: Una prueba matemática que requiere de 200 Terabytes. May 13, 2016
- Nature News: Two-hundred-terabyte maths proof is largest ever. May 26, 2016
- Popular Mechanics: World's Largest Math Proof Takes Up 200 Terabytes. May 27, 2016
- Azimuth: Very Long Proofs. May 28, 2016
- fossBytes: Pythagorean Triples — The World’s Largest Ever Math Proof Takes Up To 200TB. May 28, 2016
- Engadget: Largest-ever math proof chews up 200TB of data. May 29, 2016
- Phys.org: Computer generated math proof is largest ever at 200 terabytes. May 30, 2016
- Computational Complexity: New Ramsey Result that will be hard to verify but Ronald Graham thinks its right which is good enough for me. May 30, 2016
- Der Spiegel: Zahlenrätsel: Der längste Mathe-Beweis der Welt. May 30, 2016
- Science Alert: The world's largest maths problem has been solved, and it takes up 200 TB. May 31, 2016
- TechWorm: The largest ever supercomputer generated math proof is at 200 terabytes. May 31, 2016
- WinFuture: 200 Terabyte weisen Falschheit mathematischer Annahme nach. May 31, 2016
- Cosmos Magazine: Computer cracks 200-terabyte maths proof. May 31, 2016
- De Standaard: Wiskundig bewijs vult nationale bibliotheek. May 31, 2016
- Tom's Hardware: Problemino risolto con 200 terabyte di dati, volete provare?. May 31, 2016
- ANSA: La più lunga dimostrazione matematica di tutti i tempi. May 31, 2016
- Index: 200 ezer gigabájt a világ legbonyolultabb matematikai bizonyítása. June 1, 2016
- Tech Times: Largest Math Proof In The World Solved In 2 Days, 200 Terabytes In Size. June 2, 2016
- The Conversation: Will computers replace humans in mathematics?. June 2, 2016
- Kennislink: De tweedeling stopt bij 7824. June 3, 2016
- Jornal do Brasil: Matemáticos resolvem maior equação do mundo. June 6, 2016
- Een Vandaag (with video): Nederlandse wetenschapper lost wiskundig probleem op. June 8, 2016.
- The Aperiodical: Just how big is a big proof? June 10, 2016.
- UKNow: World's Largest Math Proof Produced at 200 Terabytes. June 13, 2016
- Heise: Zahlen, bitte! Mit 800 CPU-Kernen zur Zahl 7825. June 14, 2016
- READAROUNDYOURSUBJECT: A Super Computer for a Super Long Proof. June 22, 2016
- CNRS Le Journal: La plus grosse preuve de l’histoire des mathématiques. July 5, 2016 (english)
- Jornal du Notítias: Resolvido problema matemático com 35 anos. July 8, 2016
- Inquirer.net: Math puzzle solved, but it will take 10 billion years to verify. July 9, 2016
- Y net (with video): אחרי 35 שנה: פתרון לבעיית השלשות הפיתגורי . July 11, 2016
- ABC.se: Resuelven el problema matemático más largo del mundo: se tarda en leer 10.000 millones de años. July 11, 2016
- Daily Mail: World's longest maths proof: Solution to a 30-year-old problem would take 10 BILLION years to read - all for a prize of just $100. July 11, 2016. (youtube)
- El Diario: Resuelven problema matemático de hace 30 años. July 12, 2016
- Observador: Já foi resolvido o maior problema matemático do mundo. July 12, 2016
- Futurism: The Historical $100 Prize Has Been Awarded for a Solution That Would Take 10 Billion Years to Read. July 13, 2016
- Omicrono: Descifran un problema matemático y se tardaría 10.000 millones de años en comprobarlo. July 14, 2016
- Sina: 最长的数学证明破解了世界难题:全部阅读需100亿年. July 27, 2016
- DiarioDigitalRD: Un problema matemático de 200 terabytes. July 30, 2016
- El País: Pitágoras y la demostración de los 200 TB. September 2, 2016
- Gödel’s Lost Letter and P=NP: How Hard, Really, is SAT? September 4, 2016.
- True Viral News: The world’s largest maths problem has been solved, and it takes up 200 TB. October 2, 2016
- Motherboard: 200 Terabyte Proof Demonstrates the Potential of Brute-Force Math. July 30, 2017
Online discussions on ``largest math proof ever":
- Reddit: 250+ commments on the Nature News article
- Google+ by John Baez: 75+ comments including messages by Timothy Gowers
- Slashdot: 140+ comments on the Phys.org article
- Heise: 115+ comments.
Proof Example
Consider the problem of avoiding monochromatic solutions of the equation a + b = c with a < b < c, while coloring the natural numbers with two colors, say red and blue. This pattern cannot be avoided indefinitely. The smallest counter-example involves coloring the numbers {1, ..., 9}. This problem can be encoded into SAT using 9 Boolean variables x_i. Assigning x_i to true means putting number i in the red partition, while assigning x_i to false means putting number i in the blue partition. The DIMACS encoding of this problem is shown below.p cnf 9 32 1 2 3 0 -1 -2 -3 0 1 3 4 0 -1 -3 -4 0 1 4 5 0 -1 -4 -5 0 2 3 5 0 -2 -3 -5 0 1 5 6 0 -1 -5 -6 0 2 4 6 0 -2 -4 -6 0 1 6 7 0 -1 -6 -7 0 2 5 7 0 -2 -5 -7 0 3 4 7 0 -3 -4 -7 0 1 7 8 0 -1 -7 -8 0 2 6 8 0 -2 -6 -8 0 3 5 8 0 -3 -5 -8 0 1 8 9 0 -1 -8 -9 0 2 7 9 0 -2 -7 -9 0 3 6 9 0 -3 -6 -9 0 4 5 9 0 -4 -5 -9 0 Since this problem has 9 Boolean variables, there are 512 possible partitions. However, a refutation proof, i.e., a proof that provides a counteraxmple of all patitiones only consists of four patterns (more than a factor of 100 less). Those patterns are shown below as a DRAT proof, the format used to represent the proof of the Pythagorean Triples problem.
1 4 0 1 0 4 0 0