Convex Hull (due 06 Oct 2023)

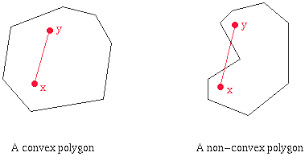
A convex hull is the smallest convex polygon that will enclose a set of points. In a convex polygon a line joining any two points in the polygon will lie completely within the polygon. One way to visualize a convex hull is as follows: imagine there are nails sticking out over the distribution of points. Place a rubber band such that it encircles all the nails. The figure described by the rubber band is a convex hull.

Convex Hull

Convex / Non-convex Polygons

Input: You will read your data from standard input. The format of the input will be as given in hull.in. The first line will be a single integer n denoting the number of points, where n will be in the range 3 to 100 inclusive. It will be followed by n lines of data. Each line will have the x and y coordinates of a point. The coordinates of the points will be integers in the range (-200, 200).

Output: For the given input you will print the vertices of the convex hull starting at the extreme left point and going clockwise around the convex hull. You will print your output to standard out as given in the following format hull.out. 

Convex Hull
(-100, -33)
(-96, 77)
(-93, 80)
(-27, 99)
(25, 100)
(77, 94)
(84, 93)
(100, 26)
(98, -83)
(69, -98)
(-15, -99)
(-95, -98)

Area of Convex Hull = 37218.0

Convex Hull for Input Data

There are many algorithms for solving the convex hull problem. You will have to implement the Graham's scan algorithm that is of order O(n log n). The algorithm is given to you in pseudo code. 

Input: A set of point objects in the x-y plane.

Output: A list of point objects that define the vertices of the convex
        hull in clockwise order.

1.  Sort the points by x-coordinates resulting in a sorted sequence
    p_1 ... p_n.

2.  Create an empty list upper_hull that will store the vertices
    in the upper hull.

3.  Append the first two points p_1 and p_2 in order into the upper_hull.

4.  For i going from 3 to n 

5.    Append p_i to upper_hull.

6.    While upper_hull contains three or more points and the last three
      points in upper_hull do not make a right turn do (refer to the
	  notes below on determinants for right and left interpretations)

7.    Delete the middle of the last three points from upper_hull

8.  Create an empty list lower_hull that will store the vertices
    in the lower hull.

9.  Append the last two points p_n and p_n-1 in order into lower_hull with
    p_n as the first point.

10. For i going from n - 2 downto 1

11.   Append p_i to lower_hull

12.   While lower_hull contains three or more points and the last three
      points in the lower_hull do not make a right turn do

13.     Delete the middle of the last three points from lower_hull

14. Remove the first and last points for lower_hull to avoid duplication
    with points in the upper hull.

15. Append the points in the lower_hull to the points in the upper_hull 
    and call those points the convex_hull

16. Return the convex_hull.

Two points p (px, py) and q (qx, qy) define a straight line. If add a third point r (rx, ry) how do you know whether r is to the right or left of the line defined by p and q. There is a simple solution to it. Evaluate the following determinant: 

1   px   py
1   qx   qy
1   rx   ry
If the determinant is zero then the three points are in a straight line. The sign of the determinant will decide if the point is to the right or left of the line. Find that for yourself.

The computation of the area of a polygon given its vertices involves computing another determinant. If the vertices of a polygon are given by [p1, p2, ..., pn] where n is greater than or equal to 3, then compute the determinant given by the coordinates of the vertices: 

x1  y1
x2  y2
..  ..
xn  yn

det = (x1 * y2 + x2 * y3 + ... + xn * y1 - y1 * x2 - y2 * x3 - ... - yn * x1)

area = (1/2) * abs (det)

Here is the template of the file Hull.py that you will be submitting. You may NOT change the names of the functions but you may add as many helper functions as needed. You will follow the standard coding conventions in Python. Your file will have a header as follows: 

#  File: Hull.py

#  Description:

#  Student Name:

#  Student UT EID:

#  Partner Name:

#  Partner UT EID:

#  Course Name: CS 313E

#  Unique Number: 

#  Date Created:

#  Date Last Modified:
You can always add more functions than those listed. Mac users will run their code on the command line as follows: 
python3 Hull.py < hull.in
Windows users will run their code on the command line as follows: 
python Hull.py < hull.in

For this assignment you may work with a partner. Both of you must read the paper on Pair Programming and abide by the ground rules as stated in that paper. If you are working with a partner then only one of you will submit the code. Make sure that in the header in Canvas that you have your name and UT EID and your partner's name and UT EID. If you are working alone then you will just have your name and your UT EID.

Use the Canvas system to submit your Hull.py file. We should receive your work by 11 PM on Friday, 06 Oct 2023. There will be substantial penalties if you do not adhere to the guidelines. Remember Python is case sensitive. The name of your file must match exactly what we have specified.

References