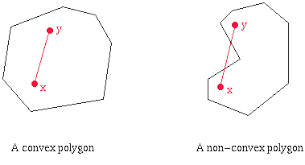
A convex hull is the smallest convex polygon that will enclose a set of points. In a convex polygon a line joining any two points in the polygon will lie completely within the polygon. One way to visualize a convex hull is as follows: imagine there are nails sticking out over the distribution of points. Place a rubber band such that it encircles all the nails. The figure described by the rubber band is a convex hull.
Input: The input will be a file called hull.in. The first line will be a single integer n denoting the number of points, where n will be in the range 3 to 100 inclusive. It will be followed by n lines of data. Each line will have the x and y coordinates of a point. The coordinates of the points will be integers in the range (-200, 200).
Output: For the input file given you will print the vertices of the convex hull starting at the extreme left point and going clockwise around the convex hull. You will write your output to a file called hull.out.
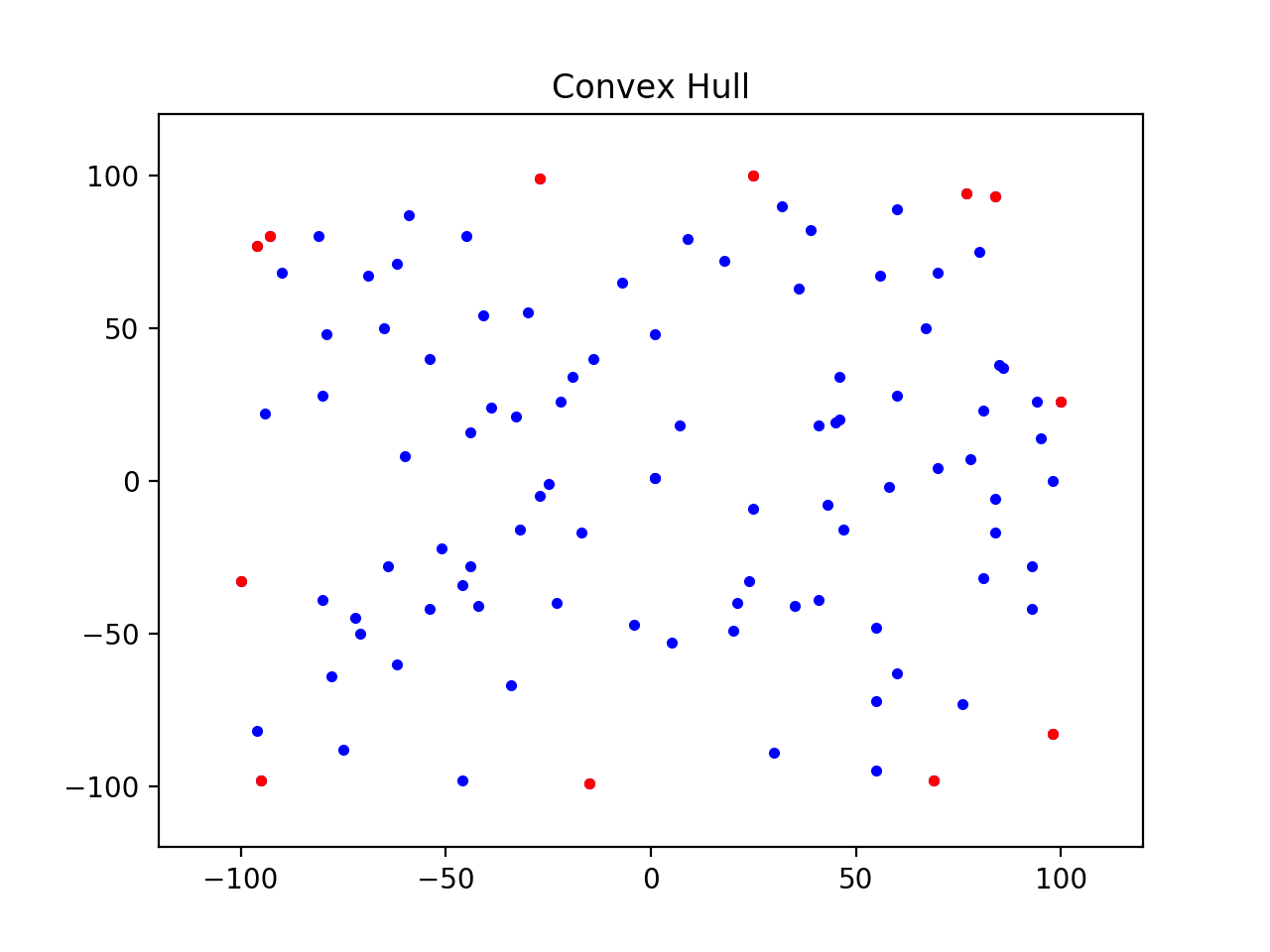
Convex Hull (-100, -33) (-96, 77) (-93, 80) (-27, 99) (25, 100) (77, 94) (84, 93) (100, 26) (98, -83) (69, -98) (-15, -99) (-95, -98) Area of Convex Hull = 37218.0
There are many algorithms for solving the convex hull problem. You will have to implement the Graham's scan algorithm that is of order O(n log n). The algorithm is given to you in pseudo code.
Input: A set of point objects in the x-y plane.
Output: A list of point objects that define the vertices of the convex
hull in clockwise order.
1. Sort the points by x-coordinates resulting in a sorted sequence
p1 ... pn.
2. Create an empty list upper_hull that will store the vertices
in the upper hull.
3. Append the first two points p1 and p2 in order into the upper_hull.
4. For i going from 3 to n
5. Append pi to upper_hull.
6. While upper_hull contains three or more points and the last three
points in upper_hull do not make a right turn do
7. Delete the middle of the last three points from upper_hull
8. Create an empty list lower_hull that will store the vertices
in the lower hull.
9. Append the last two points pn and pn-1 in order into lower_hull with
pn as the first point.
10. For i going from n - 2 downto 1
11. Append pi to lower_hull
12. While lower_hull contains three or more points and the last three
points in the lower_hull do not make a right turn do
13. Delete the middle of the last three points from lower_hull
14. Remove the first and last points for lower_hull to avoid duplication
with points in the upper hull.
15. Append lower_hull to upper_hull and call it the convex_hull
16. Return the convex_hull.
Two points p (px, py) and q (qx, qy) define a straight line. If add a third point r (rx, ry) how do you know whether r is to the right or left of the line defined by p and q. There is a simple solution to it. Evaluate the following determinant:
1 px py 1 qx qy 1 rx ryIf the determinant is zero then the three points are in a straight line. The sign of the determinant will decide if the point is to the right or left of the line. Find that for yourself.
The computation of the area of a polygon given its vertices involves computing another determinant. If the vertices of a polygon are given by [p1, p2, ..., pn] where n is greater than or equal to 3, then compute the determinant given by the coordinates of the vertices:
x1 y1 x2 y2 .. .. xn yn det = (x1 * y2 + x2 * y3 + ... + xn * y1 - y1 * x2 - y2 * x3 - ... - yn * x1) area = (1/2) * abs (det)
The file (Hull.py) that you will be submitting will have the following structure. You may NOT change the names of the functions but you may add as many helper functions as needed. You will follow the standard coding conventions in Python.
import math
class Point (object):
# constructor
def __init__(self, x = 0, y = 0):
self.x = x
self.y = y
# get the distance to another Point object
def dist (self, other):
return math.hypot (self.x - other.x, self.y - other.y)
# string representation of a Point
def __str__ (self):
return '(' + str(self.x) + ', ' + str(self.y) + ')'
# equality tests of two Points
def __eq__ (self, other):
tol = 1.0e-8
return ((abs(self.x - other.x) < tol) and (abs(self.y - other.y) < tol))
def __ne__ (self, other):
tol = 1.0e-8
return ((abs(self.x - other.x) >= tol) or (abs(self.y - other.y) >= tol))
def __lt__ (self, other):
tol = 1.0e-8
if (abs(self.x - other.x) < tol):
if (abs(self.y - other.y) < tol):
return False
else:
return (self.y < other.y)
return (self.x < other.x)
def __le__ (self, other):
tol = 1.0e-8
if (abs(self.x - other.x) < tol):
if (abs(self.y - other.y) < tol):
return True
else:
return (self.y <= other.y)
return (self.x <= other.x)
def __gt__ (self, other):
tol = 1.0e-8
if (abs(self.x - other.x) < tol):
if (abs(self.y - other.y) < tol):
return False
else:
return (self.y > other.y)
return (self.x > other.x)
def __ge__ (self, other):
tol = 1.0e-8
if (abs(self.x - other.x) < tol):
if (abs(self.y - other.y) < tol):
return True
else:
return (self.y >= other.y)
return (self.x >= other.x)
# Input: p, q, r are Point objects
# Output: compute the determinant and return the value
def det (p, q, r):
# Input: sorted_points is a sorted list of Point objects
# Output: computes the convex hull of a sorted list of Point objects
# convex hull is a list of Point objects starting at the
# extreme left point and going clockwise in order
# returns the convex hull
def convex_hull (sorted_points):
# Input: convex_poly is a list of Point objects that define the
# vertices of a convex polygon in order
# Output: computes and returns the area of a convex polygon
def area_poly (convex_poly):
# Input: no input
# Output: a string denoting all test cases have passed
def test_cases():
# write your own test cases
return "all test cases passed"
def main():
# create an empty list of Point objects
# open file hull.in for reading
# read file line by line, create Point objects and store in a list
# sort the list according to x-coordinates
# get the convex hull
# run your test cases
# open file hull.out for writing
# print the convex hull
# get the area of the convex hull
# print the area of the convex hull
if __name__ == "__main__":
main()
You can always add more functions than those listed.
For this assignment you may work with a partner. Both of you must read the paper on Pair Programming and abide by the ground rules as stated in that paper. If you are working with a partner then only one of you will submit the code. Make sure that in the header in HackerRank that you have your name and UT EID and your partner's name and UT EID. If you are working alone then you will just have your name and your UT EID.
Use the HackerRank platform to submit your code. We should receive your work by 11 PM on Friday, 03 Jul 2020. There will be substantial penalties if you do not adhere to the guidelines. HackerRank will not assign late penalties (if any), we will make the adjustments.