Notes on CS 314 Assignment 3: More Recursion and Lists

Write functions that find the sum, mean or average (mean = (sum x_i) / n), meansq (mean square = (sum x_i²) / n), variance, and stddev (standard deviation) of a list of Integer.
If the assignment does not specify it, you can use either iteration, recursion, or tail recursion (your choice). You can always use any of your functions from previous assignments, or functions from the class notes.
A formula for variance is shown below. Using the functions for mean and mean square as subroutines makes this one easy.

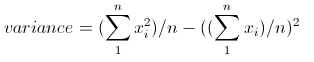
The standard deviation is the square root of the variance. You can use Math.sqrt() .
The sine function can be computed from its Taylor series expansion:
```
          1    3    5    7    9
         x    x    x    x    x
sin(x) = -- - -- + -- - -- + -- - ...
         1!   3!   5!   7!   9!
```
Write a function double sine(double x) to compute sine using this series. You may not use the functions Math.pow or factorial; instead, write a tail-recursive auxiliary function to compute each term of the series from the previous term and add it to the sum. Stop after the 21st power of x.
Hint: write down how each term of the series differs from the previous term.
Your result should be very close to Math.sin() for small values of x (say, x less than 0.6), i.e. the same for 14 digits or so.
nthcdr(int n, Cons lst) just applies rest to lst n times (cdr, pronounced "could-er", was the original name given to rest).
```
>(nthcdr 3 '(a b c d e))

(D E)
```
nthcdr is a standard function in Lisp, as are most of the rest of the functions in this assignment. If you are using Lisp, you will need to rename this function to avoid conflict. You can check whether a function name is already used with fboundp: (fboundp 'mapcar)
Write a function elt(Cons lst, int n) that retrieves the n^th item. This is a one-liner if you use nthcdr as a subroutine.
The method List.get(n) in Java is similar.
```
>(elt '(a b c d e) 3)

D
```
Write a function double interpolate(Cons lst, double x) that will make lst, a list of Integer, appear to be a continuous function by linearly interpolating for values of x.
interpolate just returns a number (it does not do any graphics).
We have values for some variable that are taken at discrete time points. For example, the newspaper publishes the temperature at each hour for the previous day. We want to know the temperature at 8:37 when what we have is temperatures at 8:00, 9:00, etc. So what we can do is to interpolate between the 8:00 and 9:00 temperatures to estimate the temperature at 8:37.
So, what we are doing is to take a set of discrete point measurements and make it look like a continuous function by connecting the dots with straight lines.
Linear interpolation is the simplest kind. There are more complex kinds of interpolation that do a better job with curvy lines.
http://en.wikipedia.org/wiki/Interpolation
Write a recursive function sumtr(Cons lst) that adds all the numbers in lst. The list lst may contain not only Integer, but also sublists, recursively.
The "tr" in the name is for "tree"; this function actually is operating on a tree with numbers at the leaves.
Actually, this function is easy. Start with the sum function that you wrote above. The only difference from the sum function is that some of the things in the list are not Integer (you can use consp to test if you found a Cons). If it is a Cons, all you need is a function to add up its contents ... don't you have such a function already?
Write a function subseq(Cons lst, int start, int end) that returns a new list that is a sub-sequence of lst beginning with the item numbered start and including items through end - 1.
subseq needs to be constructive, i.e. you need to use cons to build the output, so that you don't mess up the input. Be sure to think about using an earlier function as a subroutine.
If your technique makes the output list backwards (e.g. using tail recursion) and you want to use nreverse to get it into the right order before returning it, that is okay; this is a standard idiom, and the only exception to our rule of "no destructive functions" in assignments.
A filter is a function that allows desired elements to pass through, while removing undesired elements. Write a recursive function posfilter(Cons lst) that returns a new list containing only the non-negative values in lst, a list of Integer, in the same order as in the original list.
posfilter should be constructive.
A predicate is a boolean function, which tests its argument and returns true or false. Write a recursive function subset(Predicate p, Cons lst) that returns a new list containing only the values in lst that satisfy the predicate p. In mathematical notation, this would be written { x ∈ lst | p(x) }, pronounced the set of x in lst such that p(x). We will assume that p.pred(item) can be used to test an item.
Java does not allow a function to be passed as an argument to another function. However, it is possible to do this by making the function a method of a class and passing an element of that class as an argument.
A mapping relates an element of a set, called its domain, to an element of another set, called its range; we write M: D → R. Write a recursive function mapcar(Functor f, Cons lst) that returns a new list containing the results of applying f.fn(item) to each item in the list lst.
mapcar is important to us because it is the first half of MapReduce, a powerful system for using large numbers of computers in parallel to process large data.
Write a recursive function Object some(Predicate p, Cons lst) that returns the first item in lst that satisfies the predicate p. In mathematical notation, this would be written ∃ x p(x), and pronounced there exists an x such that p(x) or for some x, p(x).
Write a recursive function boolean every(Predicate p, Cons lst) that tests whether every item in lst satisfies the predicate p. In mathematical notation, this would be written ∀ x p(x), and pronounced for all x, p(x).